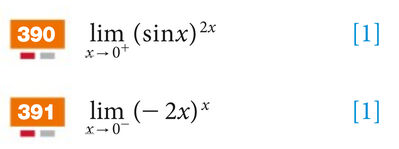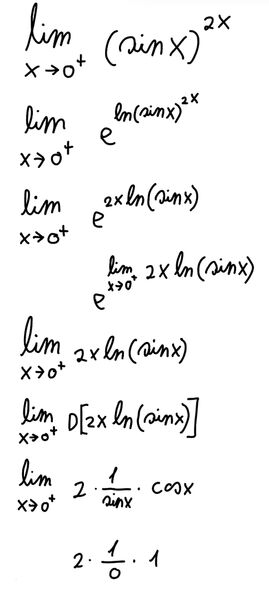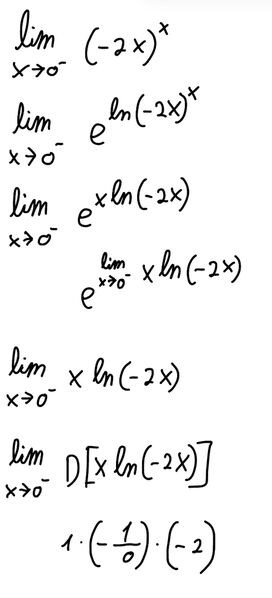In ambo gli esercizi giungo ad un punto in cui invece di ottenere un valore finito, ottengo comunque una forma indeterminata. Il che non mi permette di concludere niente. Lascio qui sotto i ragionamenti che ho fatto (spero si leggano):
390)
391)
Cos’è che in entrambi gli esercizi manca affinché si possa ottenere il famigerato valore finito?
56
punti
Livello 1
e^(2x ln sin x) = e^( ln sin x /(1/(2x)))
derivando
e^ ( 1/sin x * cos x * (-1/2x^2) ) =
= e^ [ - 2x^2 * cos x / sin x ] =
= e^ (-2 x/sin x * x cos x)
questo tende a e^(-2 * 1* 0 * 1) = e^0 = 1
l'altro : lim_x->0+ (2x)^(-x) =
= lim_x->0+ e^(-x ln 2x) =
= lim_x->0+ e^(- ln 2x /(1/x)) =
< l'Hospital >
= lim_x->0+ e^( -1/x /(-1/x^2) ) =
= lim_x->0+ e^x = e^0 = 1
47918
punti
Livello 7
