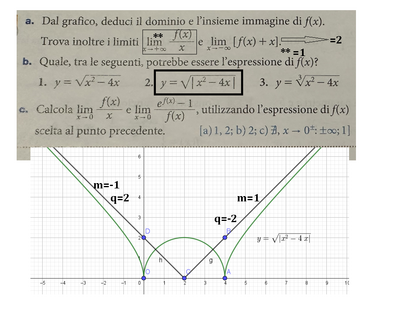
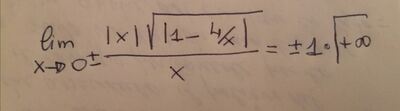a. Dal grafico, deduci il dominio e l'insieme immagine di $f(x)$.
Trova inoltre i limiti $\lim _{x \rightarrow+\infty} \frac{f(x)}{x}$ e $\lim _{x \rightarrow-\infty}[f(x)+x]$.
b. Quale, tra le seguenti, potrebbe essere l'espressione di $f(x)$ ?
1. $y=\sqrt{x^2-4 x}$
2. $y=\sqrt{\left|x^2-4 x\right|}$
3. $y=\sqrt[3]{x^2-4 x}$
c. Calcola $\lim _{x \rightarrow 0} \frac{f(x)}{x}$ e $\lim _{x \rightarrow 0} \frac{e^{f(x)}-1}{f(x)}$, utilizzando l'espressione di $f(x)$ scelta al punto precedente.
[a) 1,2 ; b) 2 ; c) $\nexists, x \rightarrow 0^{ \pm}: \pm \infty$; 1$]$