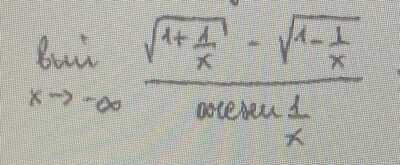Salve, ho un dubbio riguardo questo limite, esso presenta una forma indeterminata 0/0, ho pensato di risolverlo mediante funzioni asintotiche ma non so se la considerazione fatta è giusta, essa riguarda il numeratore:
conoscendo un lim notevole molto simile: (1+t)^alfa -1 è asintotico ad alfa*t avendo la t infinitesima nel punto x0. Io quindi ho visto il numeratore come questo lim notevole, poichè mi trovo (1+1/x)- una funzione che tende ad 1 nel punto 1, quindi ho riscritto il numeratore come la funzione asintotica (1/2)(1/x) ed il denominatore come 1/x, il problema è che il lim viene 1/2 e non mi trovo, quindi penso che la considerazione fatta sia sbagliata, qualcuno puó aiutarmi?