[Risolto] Leggi della dinamica

Il secondo principio della dinamica afferma che in un sistema di riferimento inerziale la somma di tutte le forze agenti su un punto materiale uguaglia la derivata della quantità di moto rispetto al tempo:
\[
\sum_{k=1}^{n} \vec{F}_{k}=\frac{d \vec{P}}{d t}
\]
dove $\vec{P}=m \vec{v}$ è la quantità di moto e $\vec{v}$ è la velocità del punto materiale. Dal momento che la massa non dipende dal tempo,
diventa:
\[
\sum_{k=1}^{n} \vec{F}_{k}=m \frac{d \vec{v}}{d t}=m \vec{a}
\]
Le forze agenti su $A$ sono $\vec{F}, N_{A}$ che è la reazione vincolare generata dal contatto $\operatorname{tra} A$ e il piano inclinato, $\vec{T}$ che è la tensione generata dalla fune che collega $A$ a $B$ ed infine la forza peso $m_{A} \vec{g} ;$ invece su $B$ agisce $-\vec{T}$ che viene generata per il terzo principio della dinamica ed è uguale ed opposta alla tensione applicata $\operatorname{su} A,$ poi $\vec{N}_{B}$ che è la reazione vincolare generata dal contatto tra $B$ e il piano inclinato ed infine la forza peso $m_{B} \vec{g}$. Scegliamo un sistema di riferimento innerziale fisso con l'origine concidente con l'inizio del piano inclinato, l'asse $x$ coincidente con l'ipotenusa del piano inclinato ed infine l'asse $y$ perpendicolare all'ipotenusa del piano inclinato.

Dalla seconda legge della dinamica per il corpo $m_{1}$ e $m_{2}$ in un generico istante $t$ possiamo scrivere il seguente sistema:
\[
\left\{\begin{array}{l}
T-m_{B} g \sin \theta=m_{B} a_{A} \\
F-T-m_{A} g \sin \theta=m_{A} a_{B}
\end{array}\right.
\]
e poichè i due punti materiali sono collegati da un filo inestensibile e di massa trascurabile abbiamo $a_{A}=a_{B}=a,$ da cui
\[
\left\{\begin{array}{l}
T-m_{B} g \sin \theta=m_{B} a \\
F-T-m_{A} g \sin \theta=m_{A} a
\end{array}\right.
\]
Ora poniamoci nell'istante in cui la tensione è massima e scriviamo $T=T_{\max }$ ottenendo $(2)$:
\[
\left\{\begin{array}{l}
T_{\max }-m_{B} g \sin \theta=m_{B} a \\
F-T_{\max }-m_{A} g \sin \theta=m_{A} a
\end{array}\right.
\]

Da $(2)_{2}$ ci ricaviamo
\[
\frac{T_{\max }-m_{B} a}{m_{B}}=g \sin \theta
\]
e sostituendolo in $(2)_{1}$ abbiamo
\[
F-T_{\max }-\frac{m_{A}}{m_{B}} T_{\max }+m_{A} a=m_{A} a
\]
da cui
\[
F=T_{\max }+\frac{m_{A}}{m_{B}} T_{\max }
\]
Dal momento che $F=2 t \mathrm{N} / \mathrm{s}$, possiamo concludere che il tempo in cui avviene la rottura è:
\[
t=\frac{T_{\max }}{2}\left(1+\frac{m_{A}}{m_{B}}\right)
\]

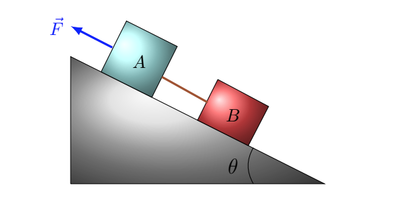
Ti premetto che non mi sembra molto chiara la traccia, soprattutto non mi torna l'espressione della forza...ma ti propongo lo svolgimento che ho pensato. 

Dobbiamo ragionare sulle forze che agiscono.

Asse x : 

• Componente parallela al piano del peso di A
• Componente parallela al piano del peso di B
• Forza F
• Tensione

Asse y : 

• Componente perpendicolare al piano del peso di A
• Componente perpendicolare al piano del peso di A
• Reazione vincolare in A
• Reazione vincolare in B

Lungo l'asse y non c'è moto, in quanto le reazioni vincolari bilanciano perfettamente le componenti perpendicolari del peso su entrambe le masse.

Ragioniamo sul moto lungo l'asse x, parallelo al piano (d'ora in poi parlando di peso mi riferisco alla sua componente parallela al piano).

Il peso di A e di B è diretto verso il basso, la forza F verso l'alto e la tensione in entrambi i versi (verso l'alto in B e verso il basso in A). Assumendo come positivo il verso della forza F, possiamo impostare le seguenti equazioni:

A: $ F=m_{A}gsin\theta+T $

B: $ T=m_{B}gsin\theta $

Sostituendo la seconda nella prima, otteniamo:

$ F=m_{A}gsin\theta+m_{B}gsin\theta \rightarrow F=gsin\theta(m_{A}+m_{B})$

Ora, il punto sta nel capire cosa succede: nel momento in cui si applica una forza su A, se il peso di B che A si porta dietro è minore della tensione, allora il sistema si muoverà verso l'alto con una certa accelerazione. Dal momento che, secondo il testo, la corda si spezza, necessariamente il peso di B deve essere maggiore di 40 N, e il sistema (almeno fino alla rottura della corda) resta in equilibrio. Per poter fare delle considerazioni matematiche, però, dobbiamo "posizionarci" nell'istante esatto in cui la corda si spezza, quindi quando il peso di B è il limite massimo sopportabile: 40 N. 

A questo punto sappiamo che:
$ F=m_{A}gsin\theta+T_{max} $, quindi la corda si spezza quando la forza supera il valore limite (che dobbiamo calcolare).

Quindi, la forza all'istante di rottura sarà pari al valore appena trovato (dipendente, quindi, anche dalla massa di A).

Per trovare il valore numerico di questo istante, basta isolare il tempo:

$ t=\frac{(m_{A}gsin\theta+40)}{2} $.

Come ti accennavo all'inizio, l'esercizio mi sembra un tantino atipico, e non vorrei aver frainteso la richiesta del problema, ma quel che ti ho descritto è ciò che accade nella situazione proposta. Per qualsiasi dubbio, chiarimento o anche per eventualmente correggere un'interpretazione erronea della traccia, fammi sapere.

La forza gravitazionale Fg = sen Θ*g*(Ma+Mb) >> della forza F al tempo to , per cui le masse scivolano inizialmente in basso con accelerazione iniziale massima per poi rallentare, fermarsi e cominciare a salire quando F comincia ad assumere l'appropriato valore .

Ha pensato a tutto questo quel genio che ha concepito 'sto problema ??