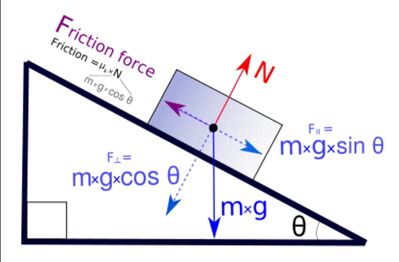
Lancio della moneta
Una moneta da $14 g$ viene lanciata e scivola verso I'alto su una superficie inclinata di un angolo di $18^{\circ}$ al di sopra dell'orizzontale. Il coefficiente di attrito dinamico fra la moneta e la superficie è 0,23 , il coefficiente di attrito statico è 0,35 . Determina il modulo, la direzione e il verso della forza di attrito:
a) quando la moneta sta scivolando;
b) dopo che la moneta si è fermata.
[a) $F_{ d }=-0,030 N$, parallela alla superficie e verso il basso:
b) $F_{ s }=0,042 N$, parallela alla superficie e verso l'alto]
L'accelerazione sugli sci
Uno sciatore di massa $65 kg$ scende da un pendio inclinato di $27^{\circ}$ rispetto all'orizzontale.
a) Calcola l'accelerazione dello sciatore nell'ipotesi che il pendio sia liscio e ghiacciato e che quindi si possa trascurare l'attrito.
b) Calcola l'accelerazione dello sciatore nell'ipotesi che il coefficiente di attrito tra gli sci e la neve sia 0,029.
(a) $4.5 m / s ^2 ;$ b) $\left.4.2 m / s ^2\right]$