Salve avrei bisogno di un aiuto con questo problema di fisica di quarto superiore.
Due sfere identiche, inizialmente neutre e di massa uguale a 40g,vengono appese a due fili verticali di lunghezza l. Successivamente le due sfere vengono caricate positivamente con un valore di carica q=3,5*10^(-6)C e raggiungono l'equilibrio quando la loro distanza è pari a "l"
Determina:
La lunghezza l dei fili e il modulo della tensione sei fili
30
punti
Livello 0
Il triangolo è equilatero. L'angolo al vertice risulta quindi essere 60 gradi e ciascun angolo alfa= 30°.
Essendo le due sfere in equilibrio, valgono le relazioni:
{T* cos(alfa) = m*g
{|Fe| = T* sin(alfa)
Dalla prima si ricava:
T= m*g/ cos(alfa)
Dalla seconda si ricava il valore di l, lato del triangolo equilatero:
l= radice [(k*Q²) /(m*g*tan(alfa)]
Quindi il lato del triangolo equilatero è:
l= 70 cm
T= 0,45 N
76753
punti
Genius II
Ciao nik, grazie per gli auguri. Li ricambio di cuore. Osservazione corretta come sempre! Buona giornata
Nelle unità SI
* m = 40 g = 1/25 kg
* g = 9.80665 = 196133/20000 m/s^2
* q = 3.5 μC = 7/2000000 C
* k = 1/(4*π*ε) ~= 1/(4*π*ε0) ~= 9*10^9 N•(m/C)^2
---------------
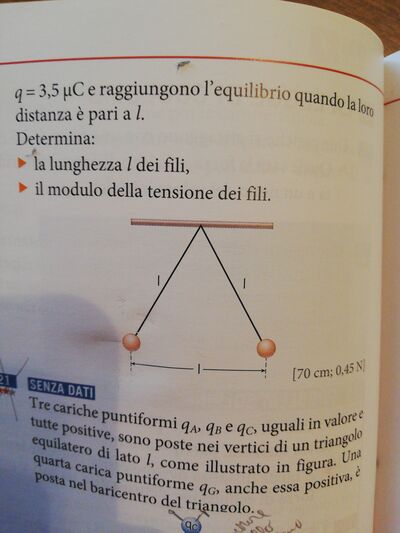
All'equilibrio le cariche sono, ai vertici di un triangolo equilatero di lato L, soggette ciascuna a una forza di Coulomb
* |F| = k*(q/L)^2 = 441/(4000*L^2) N
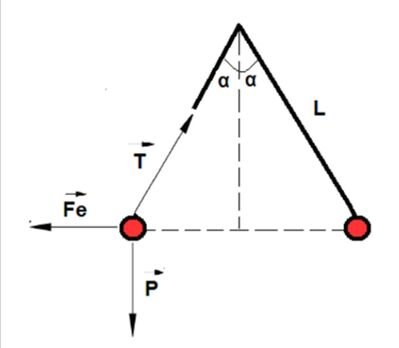
In un riferimento Oxy con y opposto alla gravità le componenti delle tre forze sono
* peso P(0, - m*g) = (0, - (1/25)*196133/20000) = (0, - 196133/500000)
* Coulomb F(441/(4000*L^2), 0)
* tensione T(x*cos(60°), x*sin(60°)) = (x/2, (√3/2)*x)
e la risultante R da azzerare è
* R = F + P + T =
= (441/(4000*L^2), 0) + (0, - 196133/500000) + (x/2, (√3/2)*x) =
= (441/(4000*L^2) + x/2, (√3/2)*x - 196133/500000)
I valori richiesti sono la soluzione del sistema che dà l'equilibrio
* (441/(4000*L^2) + x/2 = 0) & ((√3/2)*x - 196133/500000 = 0)
che però, pur producendo uno dei valori attesi (x = |T| ~= 0.45294976 N), non produce un valore reale per L.
DEVI RICONTROLLARE I CONTI CHE, evidentemente, IO HO TOPPATO.
57373
punti
Genius I
