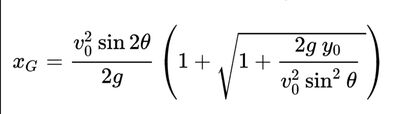Buona sera,
Ho una mezza idea di come risolvere questo esercizio ma dato che non ci sono le correzioni ho bisogno di una certezza.
Il problema è il seguente
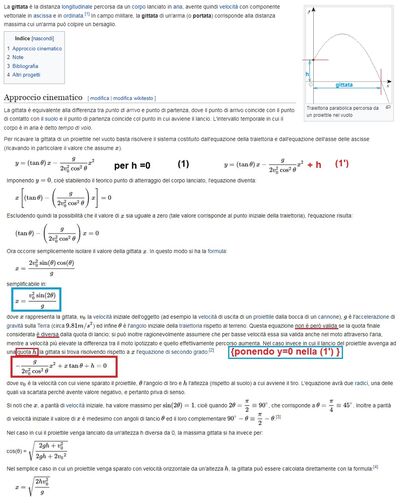
Nel lancio del peso un atleta lancia il peso con una velocita iniziale in modulo 12.2 m/s da un'altezza di 1.57 m dal suolo. calcola la gittata se l'angolo di lancio è:
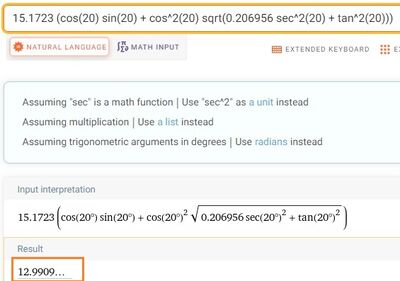
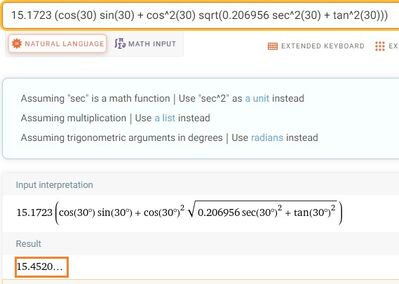
A) 20 gradi B)30 gradi C)40 gradi
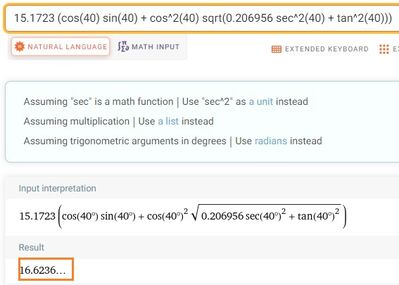
io ho pensato di risolverlo cosi:
R=(2v^2/g)*sen *cos