Buongiorno, avrei bisogno di un grande aiuto per questi esercizi di fisica che mi sono stati assegnati per le vacanze di Pasqua.
QUESITO 1
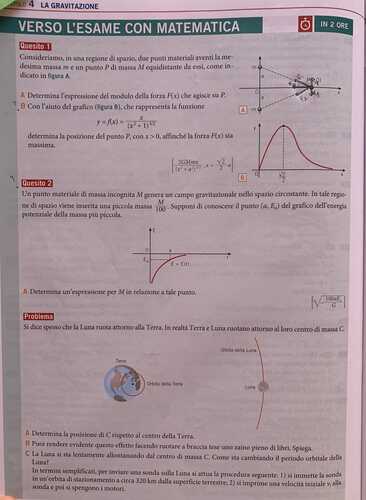
Consideriamo, in una regione di spazio, due punti materiali aventi la medesima massa $m$ e un punto $P$ di massa $M$ equidistante da essi, come indicato in figura A.
A Determina l'espressione del modulo della forza $F(x)$ che agisce su $P$.
B Con laiuto del grafico (figura B), che rappresenta la funzione
$$
y=f(x)=\frac{x}{\left(x^{2}+1\right)^{3 / 2}}
$$
determina la posizione del punto $P,$ con $x>0$, affinché la forza $F(x)$ sia massima.
$$
\left[\frac{2 G M m x}{\left(x^{2}+a^{2}\right)^{3 / 2}}, x=\frac{\sqrt{2}}{2} a\right]
$$
QUESITO 2
Un punto materiale di massa incognita $M$ genera un campo gravitazionale nello spazio circostante. In tale regione di spazio viene inserita una piccola massa $\frac{M}{100}$. Supponi di conoscere il punto $\left(a, E_{a}\right)$ del grafico dell'energia potenziale della massa più piccola.
\text { A Determina un'espressione per } M \text { in relazione a tale punto. }