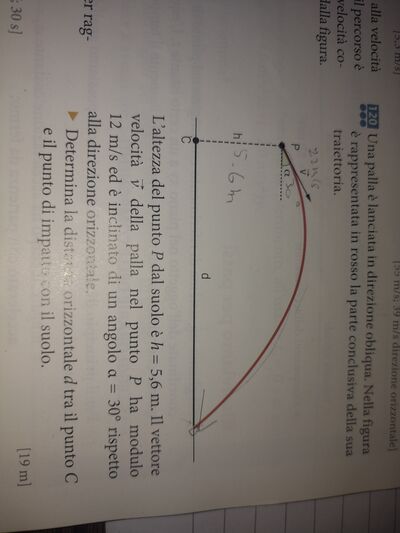
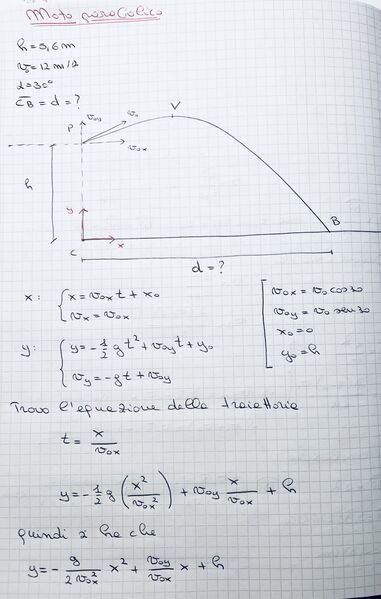
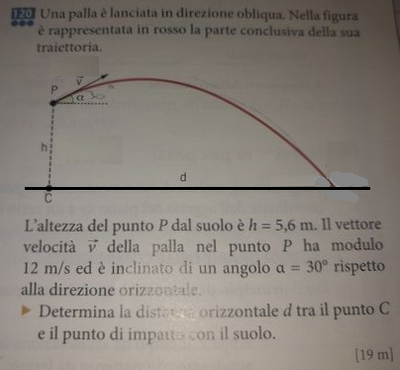
Una palla è lanciata in direzione obliqua. Nella figura è rappresentata in rosso la parte conclusiva della sua traiettoria.
L'altezza del punto $P$ dal suolo è $h=5,6 \mathrm{~m}$. Il vettore relocità $\vec{v}$ della palla nel punto $P$ ha modulo $2 \mathrm{~m} / \mathrm{s}$ ed è inclinato di un angolo $\alpha=30^{\circ}$ rispetto alla direzione orizzontale.
Determina la distanza orizzontale $d$ tra il punto $C$ e il punto di impatto con il suolo.
$[19 \mathrm{~m}]$
ho un problema in fisica