iperbole

Question

a. Scrivi l'equazione dell'iperbole riferita agli assi, con i fuochi sull'asse $x$, di eccentricità $\frac{\sqrt{5}}{2}$ e passante per $(4 \sqrt{3} ; 2)$.
b. Determina l'equazione della retta tangente nel suo punto $P$ di ascissa $2 \sqrt{10}$ e di ordinata negativa.
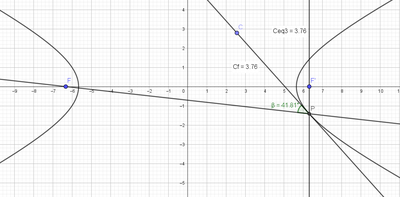
c. Dimostra che tale tangente è la bisettrice dell'angolo $F^{\prime} \widehat{P F}$, essendo $F$ e $F^{\prime}$ i fuochi dell'iperbole.
a) $\frac{x^2}{32}-\frac{y^2}{8}=1$;
b) $\sqrt{10} x+2 \sqrt{2} y-16=0]$

come faccio il punto c del n. 397?

Autore

Risposta

bibi177

(@bibi177)

38 punti

livello:

Livello 0

23 Risposte
10 0 11

20/04/2024 16:41

LucianoP · Accepted Answer

[attach]78514[/attach] x^2/α - y^2/β = 1 α = a^2 e β = b^2 e = c/a = √5/2 c = √(a^2 + b^2) γ = α + β {(4·√3)^2/α - 2^2/β = 1  passa per [4·√3, 2] {(α + β)/α = (√5/2)^2 quindi risolvo: {48/α - 4/β = 1 {(α + β)/α = 5/4 ed ottengo: [α = 32 ∧ β = 8] x^2/32 - y^2/8 = 1 γ = 32 + 8 = 40----> c = 2·√10 F( -2·√10,0) ed F'( 2·√10,0) F' ha stessa ascissa di P Calcolo ordinata di P e della retta tangente in P {x^2/32 - y^2/8 = 1 {x = 2·√10 risolvo ed ottengo: [x = 2·√10 ∧ y = √2, x = 2·√10 ∧ y = - √2] Quindi: P[2·√10, - √2] Formule di sdoppiamento: 2·√10·x/32 - (- √2)·y/8 = 1 2·√10·x + 4·√2·y - 32 = 0 √10·x + 2·√2·y - 16 = 0

LucianoP · Answer

Devi verificare che un punto qualsiasi della retta tangente trovata è equidistante dalla retta : x=2·√10 e da quella per i due punti  P ed F. Vedi sotto: [attach]78511[/attach]

exProf · Answer

Potresti iniziare rendendolo leggibile.

[Risolto] iperbole

Domande