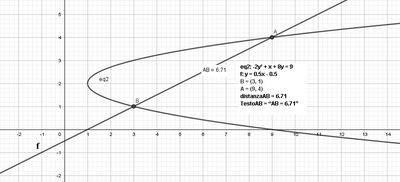
Data la parabola di equazione x = 2y^2 - 8y + 9 trovare quale retta che interseca la parabola e che ha coefficiente angolare 1/2, definisce una corda lunga 3 radical 5.
N.B. Chiedo per favore la soluzione mediante metodo algebrico con tutti i calcoli esposti, perchè ho impostato il problema, ma non riesco a finirlo, vista la complessità delle operazioni
1502
punti
Livello 1
Io la complessità non la vedo, ma ovviamente parlo a priori: mo ci provo.
---------------
La parabola
* Γ ≡ x = 2*y^2 - 8*y + 9 ≡
≡ x = 2*(y - 2)^2 + 1
ha:
* asse di simmetria y = 2, parallelo all'asse x;
* apertura a = 2 > 0, quindi concavità verso x > 0;
* vertice V(1, 2)
---------------
Il sistema fra Γ e il fascio improprio p(k) di pendenza m = 1/2
* (p(k) ≡ y = x/2 + k) & (Γ ≡ x = 2*(y - 2)^2 + 1) ≡
≡ (x = 2*(y - k)) & (2*(y - 2)^2 + 1 - x = 0)
ha risolvente
* 2*(y - 2)^2 + 1 - 2*(y - k) = 0 ≡
≡ 2*y^2 - 10*y + 2*k + 9 = 0 ≡
≡ 2*y^2 - 10*y + 2*k + 9 = 0
con discriminante
* Δ(k) = 28 - 16*k
che dev'essere positivo per dar luogo a una corda reale non nulla; quindi
* k < 7/4
* (y = x/2 + k) & (x = 2*(y - 2)^2 + 1) & (k < 7/4) ≡
≡ P(5 - 2*k - √(7 - 4*k), (5 - √(7 - 4*k))/2)
oppure
≡ Q(5 - 2*k + √(7 - 4*k), (5 + √(7 - 4*k))/2)
---------------
La lunghezza L della corda PQ dev'essere 3*√5
* |PQ| = L(k) = √(5*(7 - 4*k)) = 3*√5
da cui, successivamente,
* k = - 1/2
* P(3, 1), Q(9, 4)
* PQ ≡ p(- 1/2) ≡ y = (x - 1)/2
---------------
Vedi il grafico e il paragrafo "Solutions" al link
http://www.wolframalpha.com/input?i=%5By%3D%28x-1%29%2F2%2Cx-1%3D2*%28y-2%29%5E2%5D
------------------------------
La complessità non l'ho vista nemmeno a posteriori, ma mi sono tanto annoiato.
Al tuo posto avrei scritto "VISTA LA PALLOSITA' DELLE OPERAZIONI".
57382
punti
Genius I
@exprof Grazie per l'aiuto, ma io procedevo in modo diverso, cioè mettevo a sistema la funzione della retta y= 1/2 x + q con quella della parabola x= 2y^2 - 8y +9 ; poi andavo a sostituire nella funzione parabolica al posto di y il suo valore cioè 1/2x + q e mi trovavo a dover risolvere un'equazione di secondo grado per cercare i 2 valori di x, avendo però il parametro letterale q nelle radici. Dopo, li sostituivo nell'equazione della retta e trovavo due punti P1 e P2 con le relative coordinate; infine uguagliavo la distanza fra questi 2 punti a 3 radical 5 e avrei dovuto trovare q. Evidentemente in questa mole di calcoli, commettevo qualche errore e la soluzione non riuscivo a trovarla. Ancora ringraziamenti.
Ciao.
{x = 2·y^2 - 8·y + 9
{y = 1/2·x + q
Procedo per sostituzione: x = 2·(y - q)
2·(y - q) = 2·y^2 - 8·y + 9
2·y^2 - 8·y + 9 - 2·(y - q) = 0
2·y^2 - 10·y + 2·q + 9 = 0
Risolvo: y = (5 - √(7 - 4·q))/2 ∨ y = (√(7 - 4·q) + 5)/2
In corrispondenza ai due valori ottengo:
x = 2·((5 - √(7 - 4·q))/2 - q) ∨ x = 2·((√(7 - 4·q) + 5)/2 - q)
Determino AB^2:
AB^2 = (2·((√(7 - 4·q) + 5)/2 - q) - 2·((5 - √(7 - 4·q))/2 - q))^2 +
+((√(7 - 4·q) + 5)/2 - (5 - √(7 - 4·q))/2)^2 = (2·√(7 - 4·q))^2 + √(7 - 4·q)^2=
=(2·√(7 - 4·q))^2 + √(7 - 4·q)^2 = (3·√5)^2
Quindi:
4·(7 - 4·q) + (7 - 4·q) = 45
35 - 20·q = 45---------> q = - 1/2-------> y = x/2 - 1/2
94807
punti
Genius II
