Mi servirebbe un'aiuto su questo problema, domani ho un'interrogazione
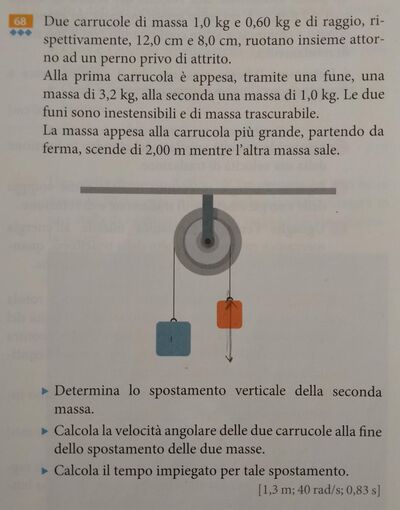
Due carrucole di massa 1,0 kg e 0,60 kg e di raggio, rispettivamente, 12,0 cm e 8,0 cm, ruotano insieme attorno ad un perno privo di attrito. Alla prima carrucola è appesa, tramite una fune, una massa di 3,2 kg, alla seconda una massa di 1,0 kg. Le due funi sono inestensibili e di massa trascurabile. La massa appesa alla carrucola più grande, partendo da ferma, scende di 2,00 m mentre l'altra massa sale.
- Determina lo spostamento verticale della seconda massa
- Calcola la velocità angolare delle due carrucole alla fine dello spostamento delle due masse
- Calcola il tempo impiegato per tale spostamento