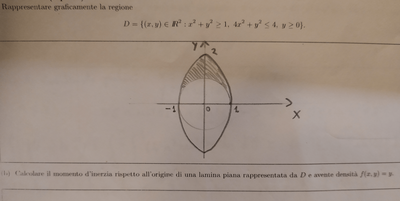
Salve a tutti, mi serve un suggerimento per calcolare il momento d'inerzia di una lamina piana. L'esercizio è diviso in due parti, nella prima bisogna disegnare il grafico della regione $D$ su cui bisogna integrare e successivamente devo calcolare il baricentro della lamina rappresentata da $D$.
Dal dominio dato ho ricavato che la regione $D$ si trova nel semipiano dato da $y>0$, compresa tra una circonferenza di raggio $1$ e un ellisse di equazione $x^2 + \frac{y^2}{4} = 1$.
So che la formula per calcolare il momento d'inerzia rispetto all'origine in $R^2$ è:
$\int{}^{}{(x^2+y^2) f(x,y) dx dy}$
Nell'esercizio la densità $f(x,y) = y$
Vorrei sapere se fin qui il ragionamento che ho fatto è giusto e sapere qual è il cambio di variabili opportuno; devo fare un cambio di coordinate polari, ellittiche, oppure mi conviene rimanere con le coordinate cartesiane $x$ e $y$?