il gabbiano

@Rob3rt4 

https://www.sosmatematica.it/forum/domande/problema-sulla-accellerazione/?orderby=votes

a) la conchiglia è soggetta all'accelerazione di gravità g verso il basso:

g = - 9,8 m/s^2;

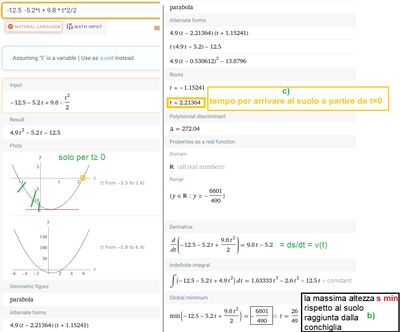
b) la conchiglia si trova a quota ho = 12,5 m e ha la velocità verso l'alto del gabbiano, vo = 5,20 m/s;

v = g * t + vo; (velocità nel moto accelerato; la conchiglia sale fino a che la velocità diventa 0 nel punto più alto raggiunto).

v = - 9,8 * t + 5,20;  poniamo v = 0, troviamo il tempo per salirre.

- 9,8 * t + 5,20 = 0

t = - 5,20 / (- 9,8) = 0,531 s, dopo questo tempo la conchiglia si ferma nel punto più alto, poi riprende a scendere.

h max = 1/2 g t^2 + vo t + ho;

h max = 1/2 * (- 9,8) * 0,531^2 + 5,20 * 0,531 + 12,5;

h max = - 1,38 + 2,76 + 12,5 = 13,88 m; (altezza massima).

c)

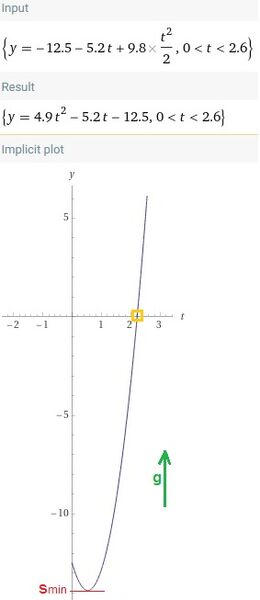
La conchiglia riparte verso il basso con velocità 0 m/s e accelerazione - 9,8 m/s^2, parte da altezza ho = 13,88 e arriva a 0 metri.

h = 1/2 g t^2 + ho;

h = 1/2 * (- 9,8) * t^2 + 13,88 ;

h = 0 metri (a terra).

- 4,9 * t^2 + 13,88 = 0;

t^2 = - 13,88 / (- 4,9); 

t = radicequadrata(13,88 / 4,9) ;

t = rad(2,83) = 1,68 s; (tempo di discesa);

d)  v = g * t + vo;

v = - 9,8 * 1,68 = - 16,46 m/s; (velocità finale, negativa perché è rivolta verso il basso).

In valore assoluto, in km/h:

v = 16,46 * 3,6 = 59 km/h. (velocità con cui arriva a terra).

Ciao  @rob3rt4

un gabbiano, salendo in verticale con una velocità Vo di 5,20 m/s lascia cadere una conchiglia quando si trova ad ho = 12,5 m da terra:

a) quali sono il modulo e il verso dell'accelerazione a della conchiglia nell'istante in cui viene lasciata?

a = g = -9,806 m/sec^2

b)qual è la massima altezza H rispetto al suolo raggiunta dalla conchiglia?

H = ho+Vo^2/2g = 12,5+5,20^2/19,612 = 13,88 m (conservazione dell'energia)

c) quanto tempo t impiega la conchiglia a ritornare a terra?

0-12,5 = Vo*t-g/2*t^2

-12,5-5,2t+4,903t^2 = 0 

t = (5,2+√5,2^2+4,903*12,5*4)/9,806 = 2,213 sec 

d) qual è la velocita V della conchiglia nell'istante in cui tocca il suolo?

V = √Vo^2+2gho  = √5,2^2+19,612*12,5 = 16,50 m/sec (conservazione dell'energia)

oppure

V = √2gH = √19,612*13,88 = 16,50 m/sec 

Buongiorno, 

Chiedo questo esercizio sempre per una mia autovalutazione e ringrazio in anticipo chi risponderà.

Il problema è il seguente: 

un gabbiano, salendo in verticale con una velocità di 5.20 m/s lascia cadere una conchiglia quando si trova a 12.5mda terra: 

a)quali sono il modulo e il verso dell'accelerazione della conchiglia nell'istante in cui viene lasciata? 

b)qual è la massima altezza rispetto al suolo raggiunta dalla conchiglia?

c)quanto tempo impiega la conchiglia a ritornare a terra? {da t = 0 }

d) qual è la velocita della conchiglia nell'istante in cui tocca il suolo? 

Grazie mille in anticipo 

..........................................

orientiamo s verso il basso con origine al suolo , la componente di g su s   è g = ~ 9.8 m/s² >0

mentre vo = - 5.2 m/s è la componente su s della  velocità iniziale vo della conchiglia ,

a)  da  tale istante solo la terra agisce su di essa quindi g è la sua accelerazione e g il suo valore

s = so + vo*t + g*t²/2  ----> s = -12.5  -5.2*t + 9.8 * t^2/2

b) per smin  azzera la derivata di s(t) 

ds/dt = v(t) = 0 ---> 9.8*t = 5.2  ---> t = 0.5306122... s ---> 26/49 s

s(t= 26/49) = -12.5  -5.2*26/49 + 9.8 * (26/49)^2/2 =~ -13.8795918367...

c)

s=0 ---> t = tf=~2.21364 s

... l'altra soluz. è per t<0 quindi da scartare.

d)

vf = v(tf≈2.21364) =~ 9.8*2.21364 - 5.2 = 16.4937 m/s

PROVO UNO SCHIFO PROFONDO VERSO ESERCIZI COME QUESTO CHE PRETENDONO D'APPLICARE LE LEGGI DEL MOTO DEL PUNTO MATERIALE ASTRATTO AD OGGETTI CONCRETI.
Ovviamente per poter applicare le equazioni del moto di un punto materiale non si può assolutamente parlare di una conchiglia lasciata cadere che flippa cadendo, il cui moto è del tutto imprevedibile: i filmati ad altissima rapidità mostrano che, oltre alla normale resistenza dell'aria dovuta alle dimensioni, il flippaggio e la differente forma delle due superficie interna ed esterna introducono forze anche angolate rispetto alla velocità, non solo opposte.
Limitandosi a un punto materiale invece il problema si riduce a quello di determinarne le leggi del moto in base ai dati: velocità di lancio verticale in alto e quota di lancio; e poi da esse calcolare quota di culmine, tempo di volo, velocità d'impatto.
------------------------------
Un punto materiale lanciato dal punto Y(0, h) con velocità di modulo V e alzo θ = π/2 ha la posizione istantanea P(0, y) data da
* y(t) = h + (V - (g/2)*t)*t
e la velocità istantanea
* v(t) = V - g*t
---------------
Il tempo di culminazione è l'istante t > 0 in cui la velocità di salita s'azzera
* v(t) = V - g*t = 0 ≡ t = V/g
e la quota di culmine è
* y(V/g) = h + (V - (g/2)*V/g)*V/g = h + V^2/(2*g)
------------------------------
In caduta libera
* y(t) = h - (g/2)*t^2
* v(t) = - g*t
---------------
Il tempo di volo è l'istante t > 0 in cui la quota s'azzera
* y(t) = h - (g/2)*t^2 = 0 ≡ t = √(2*h/g)
---------------
La velocità d'impatto pertanto è
* v(√(2*h/g)) = - g*√(2*h/g) = - √(2*g*h)
------------------------------
Con i dati del testo
* V = 5.20 = 26/5 m/s
* h = 12.5 = 25/2 m
e con il valore standard SI per g
* g = 9.80665 = 196133/20000 m/s^2
si ha
* y(t) = 25/2 + (26/5 - (196133/40000)*t)*t
* v(t) = 26/5 - (196133/20000)*t
------------------------------
RISPOSTE AI QUESITI
--------
A) Se il lanciatore procede con V costante la sola accelerazione è g, di modulo il valore standard SI (a meno che non si fornisca il valore locale) e di verso negativo in quanto discorde dall'asse della quota.
--------
B) La quota H di culmine è
* H = y(V/g) = 25/2 + (26/5)^2/(196133/10000) = 5444125/392266 ~= 13.879 m
--------
C) Il tempo T di volo fino al suolo è la somma fra il tempo di culminazione e quello di caduta libera dal culmine
* T = (V/g) + (√(2*H/g)) =
= ((26/5)/(196133/20000)) + (√((5444125/392266)/(196133/10000))) =
= 250*(416 + √435530)/196133 ~= 1.371 s
--------
D) La velocità d'impatto al suolo è, ovviamente, quella della caduta libera
* v(√(2*H/g)) = - √(2*g*H) =
= - √((196133/10000)*5444125/392266) ~= - 16.499 m/s ~= - 59.4 km/h

Vedi anche http://www.sosmatematica.it/forum/postid/53170/