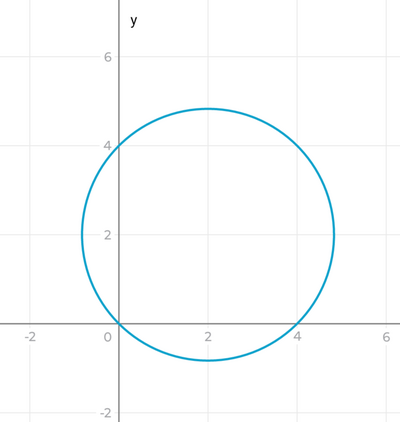
Avendo la circonferenza y=x²+y²-4x-3y e O(0;0), trovare la retta tangente alla circonferenza che passa per quel punto. so che metodo va usato se si vuole fare con il sistema e so anche la formula risolutiva, ma essendo che questo era in un test ho deciso di vedere le intersezioni della circonferenza sull'asse x e poi sull'asse y (e ci ho messo pochissimo tempo perché nel primo caso bisogna sostituire y con 0 e nel secondo x con 0) le intersezioni sono A(4;0), B(0;4) e nel mio ragionamento (non so come spiegarlo bene, spero capiate) la circonferenza è "allineata" bene in modo che l'equazione del I e III quadrante passa per il centro della circonferenza, quindi la tangente è l'equazione del II e IV quadrante (y=-x). La professoressa mi ha tolto due punti da questo test perché mi ha detto che è impossibile capire così che la retta sia quella (anche se effettivamente è quella) e non mi ha voluto fornire una spiegazione. Ciò che voglio è capire perché è impossibile capirlo così, perché adesso non è neanche un fatto di voto ma sul serio di comprensione. Vi ringrazio tutti in anticipo (allego anche una foto della circonferenza se serve)