Determina l’equazione dell’’ellisse con centro nell’origine, passante per A(1;2) e avente un vertice di coordinate (3;0). Trova poi le equazioni delle rette tangenti all’ellisse e perpendicolari alla fetta 2x-y+1=0 e calcola le coordinate dei punti di tangenza.
risultati: x2+2y2=9; x+2y+- 3rad3=0; (rad3;rad3) (-rad3; -rad3)
7
punti
Livello 0
Ciao.
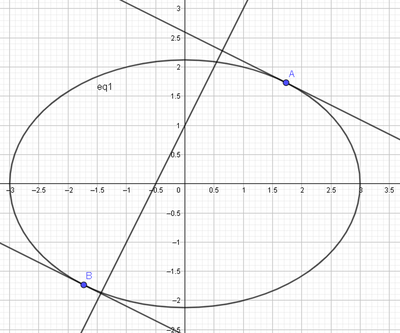
L'equazione dell'ellisse è:x^2/a^2 + y^2/b^2 = 1
Un vertice è: (3,0)------>a^2=3^2=9
Quindi l'equazione si semplifica:
x^2/9 + y^2/β = 1 ove ho posto b^2 = β
Risolvo in β imponendo il passaggio per A(1,2)
1^2/9 + 2^2/β = 1-----> 4/β + 1/9 = 1----> β = 9/2
L'equazione dell'ellisse è:
x^2/9 + 2·y^2/9 = 1
La generica retta perpendicolare a: 2·x - y + 1 = 0----->y = 2·x + 1 (m'=2,q'=1)
è: y = - 1/2·x + q (condizioni di perpendicolarità m=-1/m')
Che metto a sistema con l'ellisse trovata:
{y = - 1/2·x + q
{x^2/9 + 2·y^2/9 = 1
procedo con il metodo della sostituzione:
x^2/9 + 2·(- 1/2·x + q)^2/9 = 1
(3·x^2 - 4·q·x + 4·q^2)/18 = 1
3·x^2 - 4·q·x + (4·q^2 - 18) = 0 impongo le condizioni di tangenza: Δ/4 = 0
che si scrivono: (- 2·q)^2 - 3·(4·q^2 - 18) = 0 risolvo: 54 - 8·q^2 = 0 ed ottengo:
q = - 3·√3/2 ∨ q = 3·√3/2
da cui le due tangenti:
y = - x/2 - 3·√3/2
y = - 1/2·x + 3·√3/2
Procedo al calcolo dei punti di tangenza:
3·x^2 - 4·q·x + (4·q^2 - 18) = 0 per q = - 3·√3/2
3·x^2 - 4·(- 3·√3/2)·x + 4·(- 3·√3/2)^2 - 18 = 0
3·x^2 + 6·√3·x + 9 = 0
3·(x + √3)^2 = 0-----> x = - √3 ----> y = - (- √3)/2 - 3·√3/2----> y = - √3
Quindi: (- √3 ,- √3)
Analogamente:
3·x^2 - 4·(3·√3/2)·x + 4·(3·√3/2)^2 - 18 = 0
3·x^2 - 6·√3·x + 9 = 0-----> 3·(x - √3)^2 = 0---> x = √3
da cui: y = - 1/2·√3 + 3·√3/2---->y = √3 Quindi altro punto: ( √3, √3)
Ciao.
94774
punti
Genius II
Grazie 🙂
