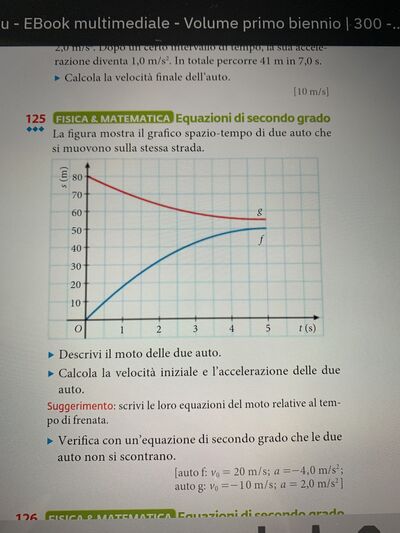
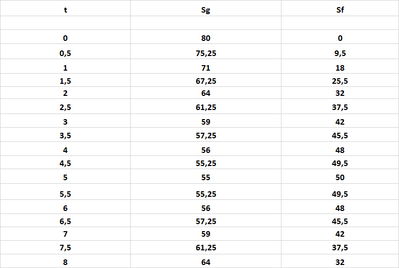
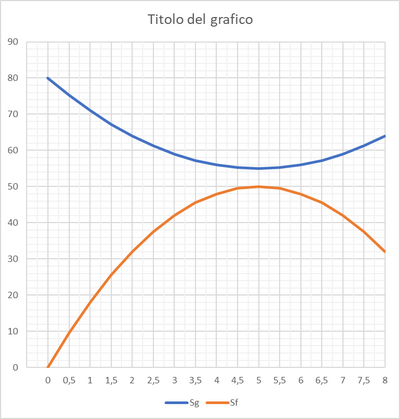
La figura mostra il grafico spazio-tempo di due auto che si muovono sulla stessa strada.
Descrivi il moto delle due auto.
Calcola la velocità iniziale e l'accelerazione delle due auto.
Suggerimento: scrivi le loro equazioni del moto relative al tempo di frenata.
- Verifica con un'equazione di secondo grado che le due auto non si scontrano.
Potreste aiutarmi con l’ultima domanda per favore?
265
punti
Livello 1
All'istante t = 5 le automobili son ferme
automobile g
-2*25 = Vg*t
Vg = -50/5 = -10,0 m/s
accelerazione ag = (0-Vg)/t = 10/5 = 2,0 m/s^2
equazione del moto
Sg = 80+Vg*t+ag/2*t^2 = 80-10*5+2/2*5^2 = 55 m
automobile f
2*50 = Vf*t
Vf = 100/5 = 20,0 m/s
accelerazione af = (0-Vf)/t = -20/5 = -4,0 m/s^2
equazione del moto
Sf = 0+Vf*t+af/2*t^2 = 0+20*5-4/2*5^2 = 50 m
Se, con quei dati iniziali , il moto proseguisse oltre i 5 s ?
114326
punti
Genius II
@remanzini_rinaldo grazie mille
Data la richiesta di utilizzare un'quazione di 2^ grado, e visto il suggerimento, io farei così
Equazione del moto di f: s = 20t +1/2(-4)t^2
Equazione del moto di g: s = -10t + 1/2(-2)t^2
Eguagliandole, avremo per quale valore del tempo i valori della posizione risulterebbero uguali, quindi in quale istante le due auto si scontrerebbero.
Abbiamo: 20t - 2t^2 = -10t +t^2
Portando tutto a sinistra, cambiando i segni e riducendo, abbiamo
3t^2 - 30 t =0
Quindi 3t(t-10) = 0 da cui 3t = 0 e t-10 =0
Una soluzione è 0, non accettabile, l'altra è t = 10, che è fuori dal campo di moto, che arriva al istante 5.
Da qui l'impossibilità che si scontrino
4268
punti
Livello 5
@giuseppe_criscuolo grazie mille
