Goniometriche

@aurora_lecchi

$tan(\alpha) \,=\, \frac{3}{4} \, \longrightarrow \, \alpha \,=\, arctan(\frac{3}{4}) \,=\, 36,87°$

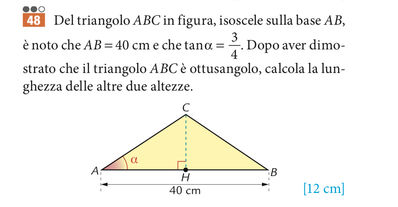
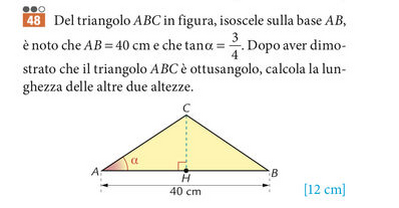
Il rapporto tra $CH$ e $AH$ equivale alla tangente dell'angolo alfa, in formula:

$\frac{CH}{AH} \,=\,tan(\alpha)$  da cui si ricava che $CH \,=\, AH \cdot tan(\alpha)$

$\longrightarrow \, CH\,=\, 20 \,cm \cdot \frac{3}{4} \,=\, 15\,cm$

Adesso verifico che il triangolo sia ottusangolo: se prendo il triangolo $AHC$ so che, essendo rettangolo, ha un angolo di $90°$ mentre $\alpha$ vale $36,87°$; la somma con l'angolo ignoto deve valere $180°$, quindi se chiamo l'angolo $x$ ho che:

$x\,=\,180°-90°-36,87°\,=\, 53,13°$

Siccome l'angolo trovato è esattamente la metà dell'angolo sul vertice $C$ trovo che l'angolo di maggior ampiezza del triangolo è $2 \cdot 53,13° \,=\,106,26°$.

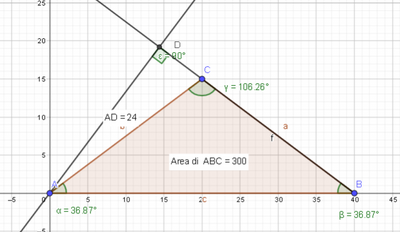
Per calcolare l'altezza relativa ai lati obliqui calcolo la lunghezza $AC \,=\,CB$ che chiamo per semplicità $L$.

Posso usare due modi:

il teorema di pitagora oppure la goniometria sapendo che $L \cdot cos(\alpha) \,=\ AH$

$L\,=\,\frac{AH}{cos(\alpha)} \,=\, \frac{20\,cm}{cos(36,87°)}\,=\,25 \,cm$

L'area $S$ del triangolo vale $\frac{40\,cm \cdot 15\,cm}{2} \,=\, 300\,cm^{2}$.

Adesso conosco la lunghezza dei lati obliqui e l'area del triangolo, l'altezza $h$ relativa a ognuno dei due lati obliqui vale:

$h \,=\, \frac{2 \cdot S}{L} \,=\, \frac{600\,cm^{2}}{25\,cm} \,=\, 24\,cm$.

@aurora_lecchi 

Di nuovo.

AH=HB= AB/2 = 20 cm

TAN(α) = CH/AH=3/4------> CH=3/4*AH=3/4·20 = 15 cm (altezza del triangolo isoscele)

Il triangolo ABC è ottusangolo perché l'angolo esterno in C è acuto ne consegue che:γ > 90°. Cioè  risulta che l'angolo esterno a questo, che è pari a 2α  corrisponde ad un angolo acuto:

TAN(2·α) = 2·TAN(α)/(1 - TAN(α)^2)=2·(3/4)/(1 - (3/4)^2)-------->TAN(2·α) = 24/7 >0

(se fosse ottuso dovrebbe risultare <0)

L'area di tale triangolo (ottusangolo) vale:

A=1/2*AB*CH=1/2·40·15 = 300 cm^2

Il lato obliquo del triangolo ABC vale: AC=BC=√(20^2 + 15^2) = 25 cm

Quindi le due altezze relative a tali lati valgono:

h=2A/AC=2·300/25 = 24 cm

@aurora_lecchi 

angolo α = arctan 3/4 = 36,87° il cui seno e coseno valgono 0,60 e 0,80 rispettivamente

angolo in C = 180-2*36,87 = 106,26° > 90° (triangolo ABC ottusangolo in C)

CH/AH = tan α = 3/4

altezza CH = 40/2*3/4 = 120/8 = 15 cm 

lato AC = √AH^2+CH^2 = 5√4^2+3^2 = 5*5 = 25 cm 

altezze BH' ed AH'' = AB*CH/AC = 40*15/25 = 40*3/5 = 24 cm 

IL RISULTATO ATTESO E' COMICAMENTE SBAGLIATO (l'area NON E' base per altezza!)
------------------------------
Come già t'ho scritto ieri sera al link
http://www.sosmatematica.it/forum/postid/32049/
«Ogni volta che di un angolo acuto di un triangolo rettangolo ti si dice che il seno o il coseno vale 3/5 o 4/5 TU DEVI RICONOSCERE la terna pitagorica (3, 4, 5) che è in proporzione con (cateto, cateto, ipotenusa).»
------------------------------
Non avevo scritto "... o la tangente vale 3/4 o 4/3 ..." ma doveva essere sottinteso!
Quindi in quest'esercizio i segmenti AC, HA, HC devono essere proporzionali a (3, 4, 5), in qualche ordine; AC, ipotenusa, prende il 5; i due cateti si devono spartire il 3 e il 4; con |HA| = 20 cm, che non è multiplo di tre, l'attribuzione è
* (|HC|, |HA|, |AC|) = (k*3, k*4 = 20 cm, k*5)
quindi
* k = 5 cm
* (|HC|, |HA|, |AC|) = (3, 4, 5)*(5 cm) = (15, 20, 25) cm
* area S(AHC) = 15*20/2 = 150 cm^2
* area S(ABC) = 2*S(AHC) = 300 cm^2
e pertanto la richiesta altezza h rispetto ai lati obliqui di ABC (lunghi 25 cm) è
* h = 2*S(ABC)/|AC| = 2*300/25 = 24 cm