Giometria Solidi

Question

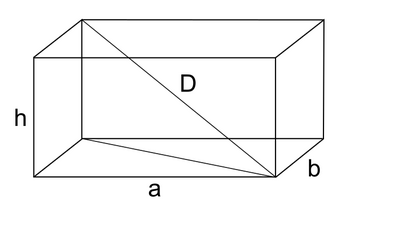
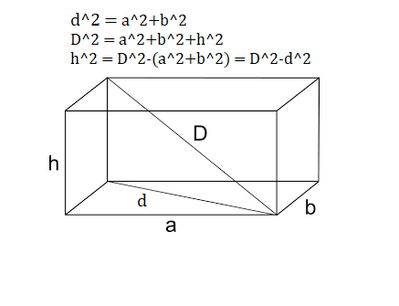
114 Il perimetro di base di un parallelepipedo rettangolo è lungo $74 cm$. Sapendo che una dimensione di base e l'altezza del solido misurano rispettivamente $22 cm$ e $10,5 cm$, calcola l'area totale.
[1437 $\left.cm ^2\right]$

115 Le dimensioni di base di un parallelepipedo rettangolo, alto $9 cm$, sono una i $\frac{3}{4}$ dell'altra e la loro somma è $56 cm$. Calcola l'area laterale e la misura della diagonale.
[1008 $\left.cm ^2 ; 41 cm \right]$

Sempre problemi con i solidi ... scusate se vi chiedo nuovamente aiuto ...

mi servirebbero il 114 e il 155 ho provato 3 volte a farli ma continuo a sbagliare il procedimento e non capisco cosa ...

Autore

Risposta

Tuasorella

(@tuasorella)

43 punti

livello:

Livello 0

34 Risposte
19 0 15

23/01/2023 22:34

remanzini_rinaldo · Accepted Answer

[attach]34909[/attach] [attach]34910[/attach] perimetro 2p = 2(a+b) = 74 cm  a = 22 cm h = 10,5 cm  b = (74/2)-a = 37-22 = 15 cm  area totale a = 2*a*b+2(a+b)*h = 22*30+74*10,5 = 1437 cm^2

gramor · Answer

115)

Parallelepipedo.

Conoscendo somma e rapporto tra le dimensioni di base puoi calcolarle come segue:

dimensione minore $= \frac{56}{3+4}×3 = \frac{56}{7}×3 = 24~cm$;

dimensione maggiore $= \frac{56}{3+4}×4 = \frac{56}{7}×4 = 32~cm$;

perimetro di base $2p_b= 2(24+32) = 2×56 = 112~cm$;

area laterale $Al= 2p_b×h = 112×9 = 1008~cm^2$;

diagonale $d= \sqrt{24^2+32^2+9^2}= 41~cm$.

gramor

(@gramor)

57898 punti

livello:

Genius I

9884 Risposte
0 3691 2131

23/01/2023 22:50

remanzini_rinaldo · Answer

[attach]34911[/attach] [attach]34912[/attach] a+3a/4 = 7a/4 = 56 cm a = 56/7*4 = 32 cm b = 56-32 = 24 cm  diagonale D = √a^2+b^2+h^2 = √32^2+24^2+9^2 = 41,0 cm  area laterale Al = 2(a+b)*h = 2*56*9 = 56*18 = 1.008 cm^2

Giometria Solidi

Domande