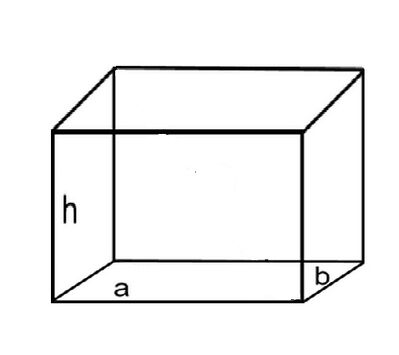
Un parallelepipedo rettangolo alto $25 \mathrm{~cm}$ ha l'area della superficie laterale che misura $2100 \mathrm{~cm}^2$. Il rapporto tra le dimensioni del rettangolo di base è $\frac{3}{4}$.
Calcola l'area della superficie totale del parallelepipedo.
[2964 $\mathrm{cm}^2$ ]
In un parallelepipedo rettangolo, il perimetro di base misura $112 \mathrm{~cm}$ e uno spigolo della base è $32 \mathrm{~cm}$. L'altezza del solido è $\frac{3}{7}$ del perimetro di base.
Determina la misura dell'area di base e quella della superficie totale del solido.
$$
\left[768 \mathrm{~cm}^2 ; 6912 \mathrm{~cm}^2\right. \text { ] }
$$
esercizio 99/100.
è da tutto il giorno che provo a farli e sinceramente sono anche un po' in crisi, perché la consegna è per domani.