Mi sembra di aver già risposto.
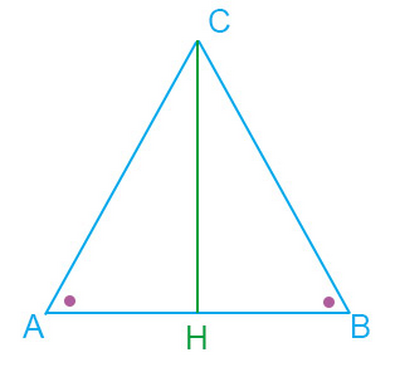
Base: triangolo isoscele
Prendi mezzo triangolo: il lato obliquo è 13/5 di metà base.
Osserva che 13 è rappresentante dell'ipotenusa e 5 è rappresentante di metà base( cateto):
√(13^2 - 5^2) = 12 è rappresentante dell'altro cateto. (altezza triangolo isoscele)
Quindi hai una terna pitagorica primitiva: (5,12,13). La tua è derivata k*(5,12,13).
Facendo riferimento alle dimensioni del triangolo isoscele invece, puoi dire che siano proporzionali ai numeri
(10,12,13) : rispettivamente base, altezza, lato obliquo
Se conosci la differenza fra lato obliquo e base:
k*(10,12,13)----> (13 - 10)·k = 9-----> k = 3
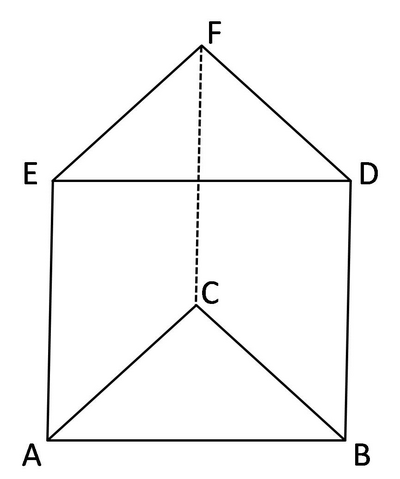
Ne consegue che le reali dimensioni di base sono: (30,36, 39) in cm (base, altezza, lato obliquo)
perimetro= 30 + 2·39 = 108 cm
area laterale=108·24 = 2592 cm^2
area di base=1/2·30·36 = 540 cm^2
Area totale=2592 + 540·2 = 3672 cm^2