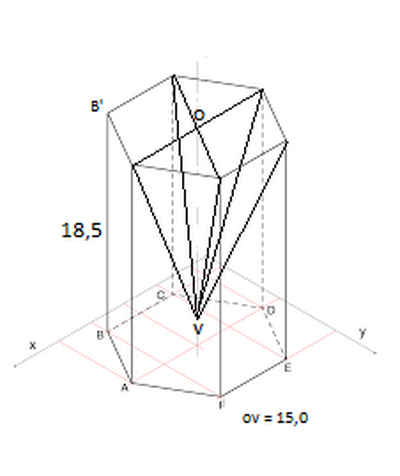
Nella base superiore di un prisma esagonale regolare è presente una cavità a forma di piramide esagonale regolare avente la base coincidente con quella del prisma. Lo spigolo di base del prisma misura 2 cm, la somma e la differenza tra l'altezza del prisma e l'altezza della piramide misurano 33,5 cm e 3,5cm. Calcola il volume del solido.
Risultato: 140,292 cm2
Qualcuno può aiutarmi?