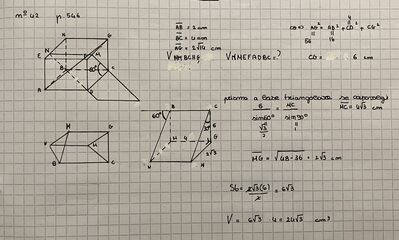
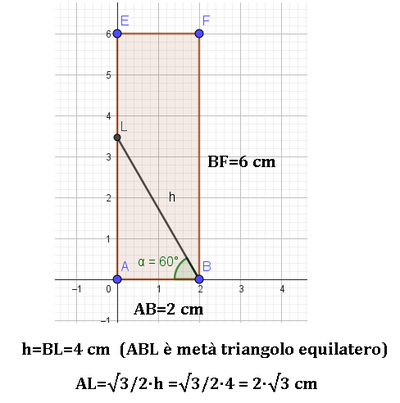
Considera un parallelepipedo di base ABCD, con AB = 2cm e BC = 4cm e diagonale lunga 2sqrt(14) cm. Un piano contenente lo spigolo BC, che forma un angolo di 60° con il piano che contiene la base ABCD, divide il parallelepipedo in due parti, di cui si chiede il volume.
Per prima cosa ho provato a trovare il volume del prisma triangolare:
- sfruttando la definizione di diagonale nel parallelepipedo ho ricavato il primo cateto della base
- usando il teorema dei seni ho ottenuto il secondo cateto, l'altezza era già data e ho trovato il volume
poi avevo intenzione di trovare il volume del parallelepipedo (ho giá le tre dimensioni 2,4,6)=> V= 48 e sottrargli il volume trovato il precedenza (che non corrisponde alle soluzione ed è sbagliato...)
Potreste spiegarmi dove ho sbagliato o propormi una soluzione alternativa, per favore? Auguro a tutti una buona giornata