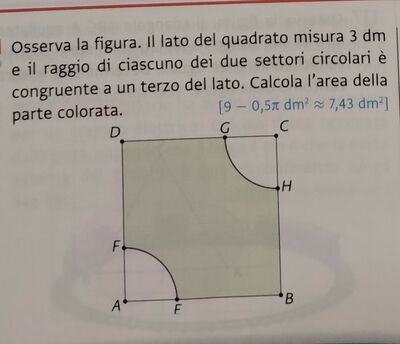
Osserva la figura. Il lato del quadrato misura $3 \mathrm{dm}$ e il raggio di ciascuno dei due settori circolari è congruente a un terzo del lato. Calcola l'area della parte colorata.
$\left[9-0,5 \pi \mathrm{dm}^2 \approx 7,43 \mathrm{dm}^2\right]$
Mi aiutate a risolvere questo problema di geometria sulle circonferenze. Grazie mille!
72
punti
Livello 1
Area parte colorata = A;
A = (Area quadrato) - (Area dei due settori);
Area quadrato = Lato^2 = 3^2 = 9 dm^2;
Raggio settore:
r = 1/3 di 3 dm;
r = 3 * 1/3 = 1 dm;
Il settore corrisponde ad un angolo di 90°; sarà 1/4 di cerchio.
Area cerchio completo = π * r^2,
Area cerchio = π * 1^2 = π dm^2; corrisponde all'angolo giro di 360°;
(Area cerchio) : 360° = (Area settore) : 90°;
π : 360° = (Area settore) : 90°;
(Area settore) = π * 90° 7 360° = π /4,
i settori da togliere sono due:
Area settori = 2 * π/4 = π/2 dm^2 = 0,5 π dm^2 ;
Area parte colorata:
A = 9 - 0,5 π dm^2;
A = 9 - 0,5 * 3,14 = 9 - 1,57 = 7,43 dm^2 (circa).
Ciao @pino-o
74770
punti
Genius II
@mg Grazie mille, chiarissimo!!!
Asett.circ.=1*3.14*90/360=0,25pi Aquad.=9 A=9-2*(0,25pi)=9-0,5pi
9852
punti
Livello 7
