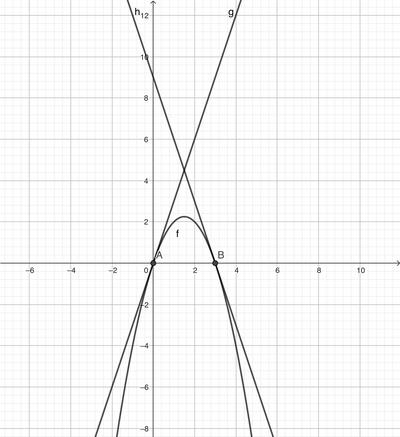
Determina le equazioni delle rette tangenti alla parabola di equazione $y=-x^2+3 x$ nei suoi punti di intersezione $A$ C $B$ con l'asse $x\left(\operatorname{con} x_A<x_B\right)$. Indica con $C$ il punto d'intersezione di tali tangenti e calcola l'area del triangolo $A B C$
$$
\left[y=3 x, y=-3(x-3) ; C\left(\frac{3}{2}, \frac{9}{2}\right) ; \frac{27}{4}\right]
$$
Salve, mi viene la retta passante per A(0,0) ma non la retta passante per B
72
punti
Livello 1
Applica le formule di sdoppiamento alla parabola:
y=-x^2+3x
in A(0,0):
y/2=3x/2———> y=3x
in B(3,0):
y/2=-3x+3(3+x)/2
y = -6x+9+3x———->y=9-3x
94792
punti
Genius II
@lucianop 👍👍
Il coefficiente angolare della retta tangente la conica (y=ax²+bx+c) nel punto (x0;y0)=(3;0) è:
m_tan= 2*a*x0 + b = 2*(-1)*(3) + 3 = - 3
Quindi la retta tangente è
y= - 3(x-3)
76754
punti
Genius II
👍
La parabola
* Γ ≡ y = - x^2 + 3*x ≡ y = x*(3 - x) ≡ y = 9/4 - (x - 3/2)^2 ≡ x^2 - 3*x + y = 0
ha
* apertura a = - 1 < 0
* zeri in A(0, 0), B(3, 0)
* Vertice V(3/2, 9/4)
quindi l'intersezione delle tangenti negli zeri è C(3/2, h), con h > 9/4, e l'area richiesta è
* S(ABC) = |xB - xA|*h/2 = (3/2)*h
---------------
La retta p, polare di C rispetto Γ, si calcola per sdoppiamento
* p ≡ x*3/2 - 3*(x + 3/2)/2 + (y + h)/2 = 0 ≡ y = 9/2 - h
e, per risultare secante Γ negli zeri, occorre e basta che si abbia h = 9/2 da cui
* C(3/2, 9/2)
* CA ≡ y = 3*x
* CB ≡ y = 3*(3 - x)
* S(ABC) = (3/2)*h = 27/4
---------------
http://www.wolframalpha.com/input?i=%5By%3D9%2F4-%28x-3%2F2%29%5E2%2Cx*y*%283*x-y%29*%283*%283-x%29-y%29%3D0%5Dx%3D-1to4%2Cy%3D-1to5
57382
punti
Genius I
@exprof 👍👍
