Sui lati dell'angolo $\widehat{O}$ in figura sono fissati i punti $A, B, C$ e $D$ in modo che $O A \cong O B$ e $A C \cong B D$. Abbiamo tracciato la semiretta $O E$ che interseca $C D$ in $F$.
Dimostra che $C F \cong F D$.
Mi potete aiutare a farlo che domani ho la verifica? Grazie
18
punti
Livello 0
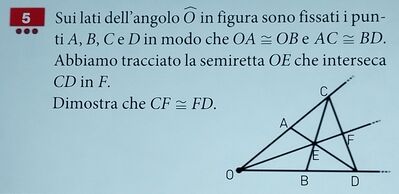
Consideriamo il triangolo OCD, esso è isoscele perché ha due lati OA+AC ed OB+BD congruenti, quindi anche i suoi angoli alla base sono congruenti.
Guardiamo ora i triangoli ACD e BDC hanno: il lato CD in comune, il lato AC congruente al lato BD (per ipotesi), e gli angoli compresi tra i due lati nominati congruenti, perché angoli alla base del isoscele OCD.
Pertanto, per il primo criterio essi sono congruenti, ed in particolare hanno gli angoli ADC e BCD congruenti, dunque EDC è triangolo isoscele e perciò CE = ED, da cui discende che, per differenza, anche AE = EB.
Allora, dei due triangoli OAE ed OBE possiamo dire che hanno OE in comune, AE=EB come dimostrato ed OA = OB (per ipotesi). Perciò per il terzo criterio sono congruenti ed OE è la bisettrice, loro e di conseguenza del triangolo ODC che, essendo isoscele, ha la bisettrice uguale alla mediana, che quindi taglia a metà la base CD, da cui la tesi CF=CD
Ciao 😉
4262
punti
Livello 5
