[Risolto] Geometria

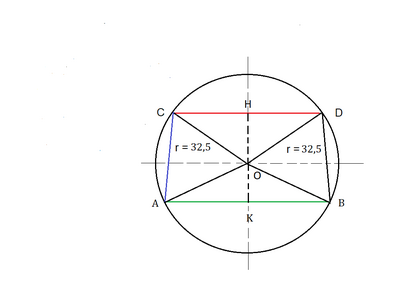
Raggio della circonferenza $r= \frac{Ø}{2} = \frac{65}{2} = 32,5 cm$.

Trapezio isoscele inscritto nella circonferenza:

hai la somma delle due corde che sono le due basi $(119 cm)$ e il rapporto tra esse $(\frac{8}{9})$ quindi un modo per calcolarle può essere il seguente:

corda CD = base minore $b= \frac{119}{8+9}×8 = \frac{119}{17}×8 = 56 cm$;

corda AB = base maggiore $B= \frac{119}{8+9}×9 = \frac{119}{17}×9 = 63 cm$;

dist. base minore dal centro $= \sqrt{32,5²-(\frac{56}{2})²} = \sqrt{32,5²-28²}  cm$;

dist. base maggiore dal centro $= \sqrt{32,5²-(\frac{63}{2})²} = \sqrt{32,5²-31,5²} = 8  cm$;

altezza $h= 16,5+8 = 24,5 cm$;

infine l'area:

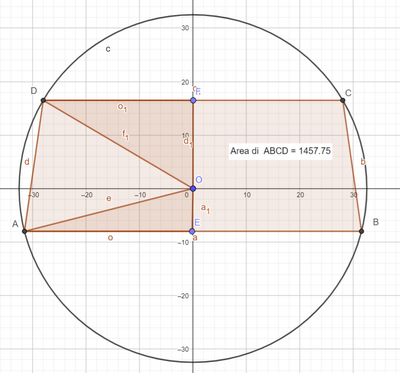
$A= \frac{(B+b)×h}{2} = \frac{(63+56)×24,5}{2} = 1457,75 cm²$;

trasforma in decimetri $A= 1457,75×10⁻² ≅  14,58 dm²$.

Due corde AB e CD, parallele e situate da parti opposte rispetto al centro di una circonferenza, sono tali che la loro somma misura 119 cm e CD è 8/9 di AB. Se il diametro della circonferenza misura 65 cm,  qual è il l'area del trapezio ABCD, espressa in decimetri quadrati?

AB+8AB/9 = 119

17AB = 119*9

AB = 119*9/17 = 63,0 cm

CD = 63*8/9 = 56 ,0 cm 

OH = √32,5^2-28^2 = 16,50 cm 

OK = √32,5^2-31,5^2 = 8,00 cm 

area A = 119*(16,50+8)/200 = 14,5775 dm^2

Come unità di misura uso cm e cm^2, non le scrivo accanto a ogni numero.
------------------------------
Se di due valori incogniti (0 < a < b) sono dati la somma (s = a + b) e il rapporto (k = a/b = m/n) allora essi sono dati da
* a = (m/(m + n))*s
* b = (n/(m + n))*s
sono i cosiddetti "problemini" di calcolo delle frazioni (IV elementare).
------------------------------
In una circonferenza qualsiasi fra il raggio "r", una qualsiasi corda "c", e la sua distanza "d" dal centro vale la relazione pitagorica
* r^2 = d^2 + (c/2)^2
------------------------------
NEL CASO IN ESAME
Con le basi da parti opposte rispetto al centro, l'altezza h del trapezio è la somma delle loro distanze dal centro.
* "diametro della circonferenza" = 65
* r = 65/2
* d = √(r^2 - (c/2)^2) = √((65/2)^2 - (c/2)^2)
---------------
Con
* s = 119
* k = a/b = 8/9
si ha
* a = (8/(8 + 9))*119 = 56
* b = (9/(8 + 9))*119 = 63
---------------
Corda AB
* c = 63
* d = √((65/2)^2 - (63/2)^2) = 8
---------------
Corda CD
* c = 56
* d = √((65/2)^2 - (56/2)^2) = 33/2
---------------
Trapezio ABCD
L'area S è il semiprodotto fra altezza h e media delle basi m
* h = 8 + 33/2 = 49/2
* m = 119/2
* S = (49/2)*119/2 = 5831/4 = 1457.75 cm^2 = 14.5775 dm^2
Per ottenere i richiesti dm^2 s'è ritratto di due cifre il separatore decimale.

x= misura corda maggiore

8/9*x= misura corda minore

---------------------------- (sommo)

17/9·x = 119--------------> x = 63 cm    semicorda=63/2 = 31.5 cm

8/9·63 = 56 cm          semicorda=56/2 = 28 cm

raggio circonferenza=65/2=32.5 cm

Con Pitagora calcolo le due distanze dal centro:

√(32.5^2 - 31.5^2) = 8 cm

√(32.5^2 - 28^2) = 16.5 cm

Altezza trapezio=8+16.5= 24.5 cm

Area trapezio (isoscele)=1/2·(63 + 56)·24.5 = 1457.75 cm^2

in dm^2------> 14.5775 dm^2