Ciao. Non mi vengono questi tre problemi. Il 296, 147,196 e 224. Grazie
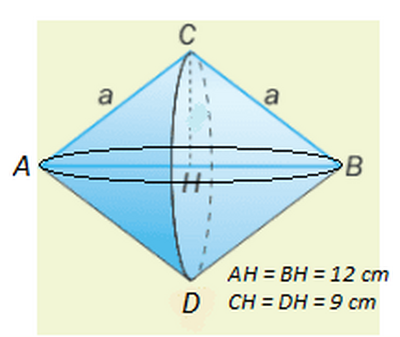
147. Un triangolo rettangolo ha i cateti lunghi rispettivamente $9 \mathrm{~cm}$ e $12 \mathrm{~cm}$. Calcola l'area totale dei due coni $C_1$ e $C_2$ che si ottengono facendo ruotare il triangolo una volta attorno al cateto maggiore $\left(C_1\right)$ e una volta attorno al cateto minore $\left(C_2\right)$. Quale dei due ha la superficie maggiore?
$\left[216 \pi \mathrm{cm}^2 ; 324 \pi \mathrm{cm}^2\right]$
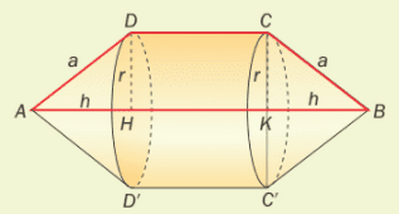
224. Un solido è costituto da un cilindro e da due coni congruenti aventi per basi le basi del cilindro. II raggio di base e l'apotema di ciascun cono misurano rispettivamente $18 \mathrm{~cm}$ e $30 \mathrm{~cm}$. L'altezza del cilindro è $\mathrm{i} \frac{4}{3}$ dell'altezza di ciascun cono. Calcola il volume del solido.
$\left[15552 \pi \mathrm{cm}^3\right]$
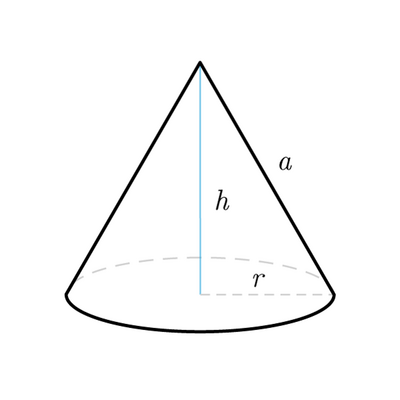
196. Calcola l'area totale e il volume di un cono equilatero avente il raggio di $12 \mathrm{~cm}$. $\left[432 \pi \mathrm{cm}^2 ; 576 \pi \sqrt{3} \mathrm{~cm}^3\right]$
296. In una piramide quadrangolare regolare la somma dell'altezza e dell'apotema misura $64 \mathrm{~cm}$ e il loro rapporto è $\frac{15}{17}$. Calcola il volume.
[10 $\left.240 \mathrm{~cm}^3\right]$