Il grafico rappresenta la funzione $f(x)$ di equazione
$$
y=\ln \frac{x^2+a x+b}{x+c} .
$$
a. Determina $a, b, c$.
b. Studia il segno di $f(x)$ e calcola i limiti agli estremi del dominio.
Ho bisogno di aiuto per risolvere il s6. Ho trovato x=-2, x=0 e x=3 che sono asintoti verticali. Ora che dovrei fare?
162
punti
Livello 1
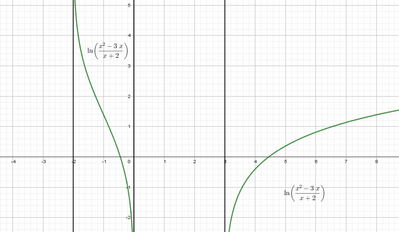
Determiniamo a,b,c
Come giustamente hai detto: asintoti verticali: x=-2; x=0; x=3. (dalla figura)
Definisci ora il C.E. : -2 < x < 0 v 3 < x < +∞
Quindi devi determinare le condizioni agli estremi del C.E. osservando la figura:
LIM(LN((x^2 + a·x + b)/(x + c)))= +∞
x---> -2+
Quindi:
LIM(LN((2·a - b - 4)/(2 - c))) = +∞
x---> -2+
Poi
LIM(LN((x^2 + a·x + b)/(x + c)) = -∞
x----> 0-
Quindi:
LIM(LN(b/c)) = -∞
x----> 0-
Poi
LIM(LN((x^2 + a·x + b)/(x + c)))= -∞
x--->3+
Quindi:
LIM(LN((3·a + b + 9)/(c + 3))) = -∞
x--->3+
Altra condizione che però è superflua è:
LIM(LN((x^2 + a·x + b)/(x + c))= +∞
x----> +∞
(in quanto dipende solo dai termini di grado max presenti al numeratore ed al denominatore della frazione)
Il primo limite in grassetto è verificato solo se c =2
Il secondo limite in grassetto è verificato solo se b=0
Quindi:
LIM(LN((3·a + b + 9)/5)) = -∞
x--->3+
cioè
LIM(LN((3·a + 0 + 9)/5)) = -∞
x--->3+
deve essere poi: 3·a + 9 = 0----> a = -3
La funzione è: y = LN((x^2 - 3·x)/(x + 2))
Per quanto riguarda il segno:
LN((x^2 - 3·x)/(x + 2)) > 0 se -2 < x < 2 - √6 ∨ x > √6 + 2
LN((x^2 - 3·x)/(x + 2)) < 0 se 3 < x < √6 + 2 ∨ 2 - √6 < x < 0
LN((x^2 - 3·x)/(x + 2)) = 0 se x = 2 - √6 ∨ x = √6 + 2
(x = 4.449489742 ∨ x = -0.4494897427)
94882
punti
Genius II
@lucianop non ho compreso come arrivi ad affermare che il primo limite sia verificato per c=2 e il secondo per b=0. Potresti spiegarmelo per favore?
