Avrei bisogno di aiuto con questo esercizio :
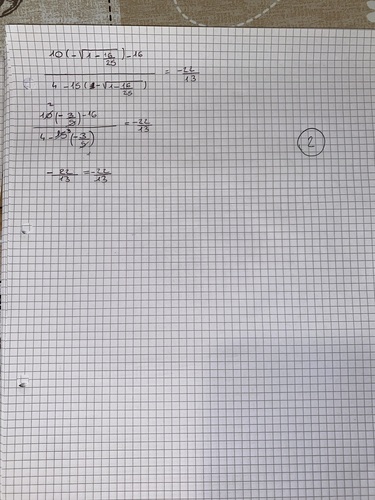
Se $\sec \alpha=\frac{5}{4}$ e $\frac{3}{2} \pi<\alpha<2 \pi,$ verifica che $\frac{2 \sin \alpha-4 \cos \alpha}{\cos \alpha-3 \sin \alpha}=-\frac{22}{13}$
(purtroppo non c'è il risultato quindi non so neanchè quale sia :c )
140
punti
Livello 1
@mr-tempesta03 prima di tutto devi soffermarti a leggere il testo. E’ chiaro che non ci sia risultato perché l’esercizio chiede ‘data la secante di un certo angolo verifica che la relazione e’ giusta quindi non si cerca un valore come risultato ma si deve dimostrare che la relazione sia un’uguaglianza ... detto questo ti allego lo svolgimento che ti ho fatto cercando di evidenziare tutti i passaggi... cerca di capirlo
12908
punti
Livello 7
@cenerentola grazie mille, sei stato molto chiara
👍😀
Risultato della verifica di un'identità è "Falso" oppure "Vero".
Se
* 3*π/2 < α < 2*π
vuol dire che, nel cerchio goniometrico, α è all'interno del quarto quadrante con seno negativo e coseno positivo.
Se
* sec(α) = 5/4
vuol dire che
* cos(α) = 4/5
* sin(α) = - √(1 - (4/5)^2) = - 3/5
e che pertanto
* (2*sin(α) - 4*cos(α))/(cos(α) - 3*sin(α)) =
= (2*(- 3/5) - 4*4/5)/(4/5 - 3*(- 3/5)) =
= (- 22/5)/(13/5) =
= - 22/13
che verifica l'identità.
57383
punti
Genius I
@exprof grazie mille
