Salve a tutti...
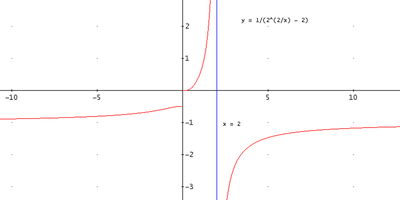
Ho questa funzione: y=1/(2^(2/x) - 2) e devo calcolare la positività.
Sono partita dal dominio.Ho trovato, dopo aver svolto l’equazione esponenziale, (-oo,0[ U ]0,2[ U ]2,+oo).
Dopo ho posto la funzione >=0 per trovare la positività.
N>=0 : sempre.
D>0 è un’equazione esponenziale. Ho ottenuto x>2.
Per cui, per me, la funzione è positiva per x>2.
Però non mi trovo con il risultato che è 0<x<2.
Vorrei capire dove sbaglio. Grazie.
229
punti
Livello 1
Mi sto davvero scervellando e non riesco proprio a capire da dove possa essere venuto fuori 0. 😅
@cmc grazie mille.
Effettivamente non avevo pensato al fatto che x è un’incognita e può essere sia positiva che negativa.
sino alla riga "N>=0 : sempre." va tutto bene.
D > 0
Consideriamo i due casi:
2^(2/x) > 2
2/x > 1
x < 2
Tenuto conto della condizione x>0 avremo la soluzione del caso
0 < x < 2.
2^(2/x) > 2
2/x > 1
2/x - 1 > 0
(2-x)/x > 0
Impossibile!
Il numeratore è positivo e il denominatore è negativo
La sola soluzione valida è
0 < x < 2
10304
punti
Livello 3
CI DEV'ESSERE UN EQUIVOCO ("svolto l'equazione esponenziale", "è un'equazione esponenziale").
La funzione
* y = 1/(2^(2/x) - 2) = 1/(4^(1/x) - 2)
NON E' AFFATTO UN'ESPONENZIALE: la variabile è indice di radice, non esponente.
Un'esponenziale sarebbe definita ovunque, e questa è indefinita in zero (la radice zeresima è insensata) e in due (il denominatore nullo è insensato).
Risulta positiva là dove
* 4^(1/x) > 2
Ora, calcolando i limiti
* lim_(x → ± ∞) 4^(1/x) = 1
* lim_(x → 0-) 4^(1/x) = 0
* lim_(x → 0+) 4^(1/x) = ∞
e tracciando un grafico
http://www.wolframalpha.com/input/?i=asymptotes+y%3D4%5E%281%2Fx%29
si vede che
* x < 0 ==> 0 < 4^(1/x) < 1
* x = 0 ==> 4^(1/x) indefinita
* x > 0 ==> 4^(1/x) > 1
e pertanto l'intervallo di positività DEVE iniziare con "(0, ...".
57382
punti
Genius I
Ciao.
prima il C.E.
{x ≠ 0 per esistenza dell'esponente
{2^(2/x) - 2 ≠ 0 per esistenza del denominatore
Quindi dal sistema: [x ≠ 2 ∧ x ≠ 0]
ossia ]-inf;0[U]0;2[U]2;+inf[
La funzione non si annulla mai perché il numeratore è 1>0
Quindi: y>0 se:
2^(2/x) - 2 > 0------>2^(2/x) > 2 stessa base 2 >0 positiva; quindi il confronto lo devi fare sugli esponenti:
2/x>1
x<0 non va bene perché otteresti una disuguaglianza assurda quindi deve essere x>0!
Se è così tranquilli: 2>x----> x>2.
Tenendo conto di queste due ultime condizioni, per forza devi avere: 0 < x < 2
Ciao
P.S. Ti allego il grafico della funzione.
94774
punti
Genius II
