Salve chi mi spiega questo
grazie
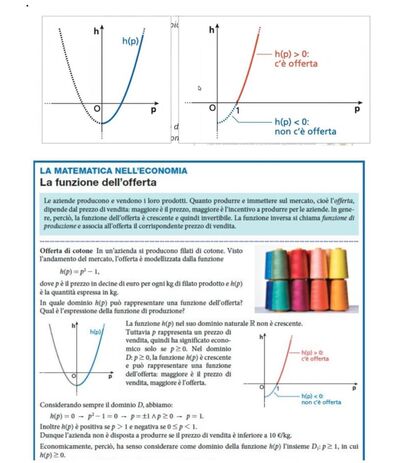
LA MATEMATICA NELL'ECONOMIA La funzione dell'offerta
Le aziende producono e vendono I loro prodotti. Quanto produrre e immettere sul mercato, cioè l'offerta, dipende dal prezzo di vendita: maggiore è il prezzo, maggiore è rincentivo a produrre per le aziende. In genere, perciò, la funzione dell'offerta è crescente e quindı invertibile. La funzione inversa si chiama funzione di produzione associa all'offerta il corrispondente prezzo di vendita.
Offerta di cotone In un'azienda si producono filati di cotone. Visto l'andamento del mercato, l'offerta è modellizzata dalla funzione
$$
h(p)=p^2-1,
$$
dove $p$ è il prezzo in decine dl euro per ogni $kg$ di filato prodotto $h (p)$ è la quantità espressa in $kg$.
In quale dominio $h(p)$ può rappresentare una funzione dell'offerta? Qual è l'espressione della funzione di produzione?
La funzione $h(p)$ nel suo dominio naturale $R$ non è crescente. Tuttavia $p$ rappresenta un prezzo di vendita, quindi ha significato economico solo se $p \geq 0$. Nel dominio D. $p \geq 0$, la funzione $h(p)$ è crescente e può rappresentare una funzione dell'offerta: maggiore è il prezzo di vendita, maggiore è l'offerta.
Considerando sempre il dominio $D$, abbiamo:
$$
h(p)=0-p^2-1=0 \rightarrow p= \pm 1 \wedge p \geq 0 \rightarrow p=1 .
$$
Inoltre $h(p)$ è positiva se $p>1$ e negativa se $0 \leq p<1$.
Dunque l'azienda non è disposta a produrre se il prezzo di vendita è inferiore a 10 € / kg.
Economicamente, perciò, ha senso considerare come dominio della funzione $h(p)$ l'insieme $D_1: p \geq 1$, in cui $h(p) \geq 0$.