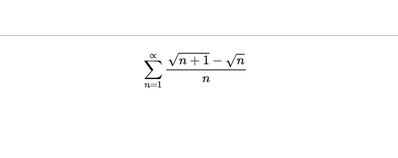
Salve, devo applicare applicare il criterio del confronto asintotico per determinare il carattere di questa seria, ma sono confuso. Come faccio a determinare la funzione asinotstica in questo? Qualcuno mi può aiutare? Grazie mille
\sum_{n=1}^{\propto}{\frac{\sqrt{n+1}-\sqrt{n}}{n}}
65
punti
Livello 1
Ti potrei aiutare se sapessi leggerla. Purtroppo se Latex fallisce é peggio che non usarlo.
47869
punti
Livello 7
doppio?
Ok è facile. La serie converge. Infatti razionalizzando il termine generale si riscrive
(n+1-n)/(n*(sqrt(n+1)+sqrt(n))
che va come 1/(n*2sqrt(n)) =
= 1/2 * 1/n^(3/2)
che è una p-serie con p>1
e come tale convergente.
Termini positivi e decrescenti a zero; direi come 1/√n.
57383
punti
Genius I
