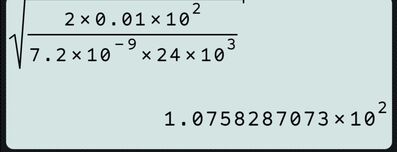Una particella con carica elettrica $7,2 \times 10^{-9} \mathrm{C}$ e massa $10 \mathrm{~g}$, inizialmente ferma, viene messa in moto da un campo elettrico uniforme e percorre una distanza di $10 \mathrm{~m}$. La differenza di potenziale tra i punti di partenza e di arrivo è $24 \times 10^3 \mathrm{~V}$. Trascura l'effetto della gravità.
Calcola il tempo impiegato dalla carica $q$ a coprire quella distanza.
$\left[1,1 \times 10^2 s\right]$
438
punti
Livello 1
Moto uniformemente accelerato con velocità iniziale nulla
S= (1/2)*a*t²
Da cui si ricava il tempo:
t= radice [(2S)/a]
La forza elettrostatica è
{ F=q*E = q*DV/S
Dal secondo principio della Dinamica
{F=ma
Da cui si ricava il valore dell'accelerazione
a= (q*DV) /(m*S)
Quindi:
t= radice [ (2 *m*S²) /(q*DV)]
Sostituendo i valori numerici otteniamo:
t= 1,1*10² s
76754
punti
Genius II
forza F = E*Q = Q*ΔV/d = 7,2*10^-9*24*10^3/10 = 1,728*10^-5 N
accelerazione a = F/m = 1,728*10^-5 N / 10^-2 = 1,728*10^-3 m/sec^2
distanza 2d = 20 = a*t^2
tempo t = √2d/a = √20*10^3/1,728 = 1,08*10^2 sec
114494
punti
Genius II
