Buonasera, ho difficoltà con questo problema, potreste aiutarmi per favore o anche dirmi come lo risolvereste? Tra un po' ho l'esame...grazie in anticipo a chi può
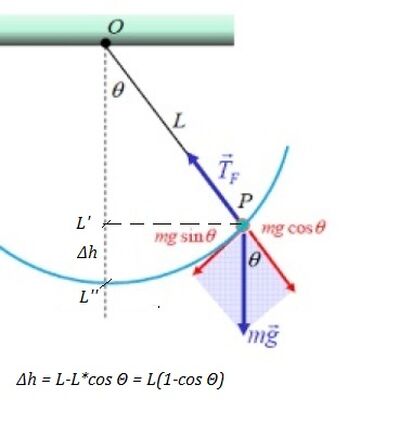
Un pendolo è costituito da un filo inestensibile di lunghezza L e massa trascurabile, alla cui estremità è appesa una pallina di massa m=150 g; il pendolo viene lasciato libero di oscillare, con velocità iniziale nulla, da una posizione in cui il filo forma un angolo α con la verticale; la massima tensione che può sopportare il filo prima di rompersi è T= 3,7 N. Il valore massimo consentito all'angolo α senza che il filo si rompa quando passa per la posizione verticale è: