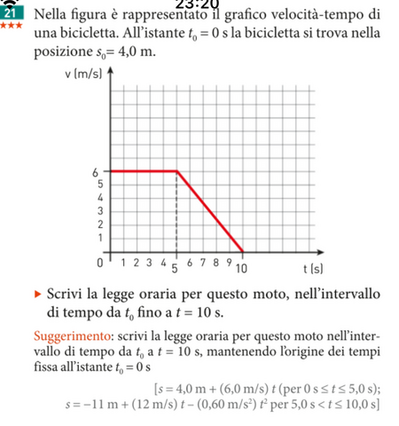
Nella figura è rappresentato il grafico velocità-tempo di una bicicletta. All'istante $t_0=0 \mathrm{~s}$ la bicicletta si trova nella posizione $s_0=4,0 \mathrm{~m}$.
Scrivi la legge oraria per questo moto, nell'intervallo di tempo da $t_0$ fino a $t=10 \mathrm{~s}$.
Suggerimento: scrivi la legge oraria per questo moto nell'intervallo di tempo da $t_0$ a $t=10 \mathrm{~s}$, mantenendo lorigine dei tempi fissa all'istante $t_0=0 \mathrm{~s}$
$$
\begin{array}{r}
{[s=4,0 \mathrm{~m}+(6,0 \mathrm{~m} / \mathrm{s}) t(\operatorname{per} 0 \mathrm{~s} \leq t \leq 5,0 \mathrm{~s})} \\
\left.s=-11 \mathrm{~m}+(12 \mathrm{~m} / \mathrm{s}) t-\left(0,60 \mathrm{~m} / \mathrm{s}^2\right) t^2 \text { per } 5,0 \mathrm{~s}<t \leq 10,0 \mathrm{~s}\right]
\end{array}
$$
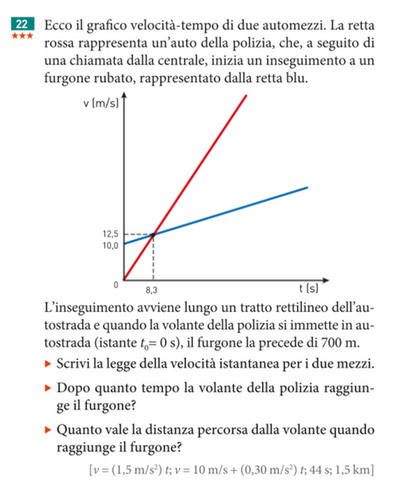
Ecco il grafico velocità-tempo di due automezzi. La retta rossa rappresenta un'auto della polizia, che, a seguito di una chiamata dalla centrale, inizia un inseguimento a un furgone rubato, rappresentato dalla retta blu.
L'inseguimento avviene lungo un tratto rettilineo dell'autostrada e quando la volante della polizia si immette in autostrada (istante $t_0=0 \mathrm{~s}$ ), il furgone la precede di $700 \mathrm{~m}$.
- Scrivi la legge della velocità istantanea per i due mezzi.
Dopo quanto tempo la volante della polizia raggiunge il furgone?
- Quanto vale la distanza percorsa dalla volante quando raggiunge il furgone?
$$
\left[v=\left(1,5 \mathrm{~m} / \mathrm{s}^2\right) t ; v=10 \mathrm{~m} / \mathrm{s}+\left(0,30 \mathrm{~m} / \mathrm{s}^2\right) t ; 44 \mathrm{~s} ; 1,5 \mathrm{~km}\right]
$$
Il numero 21, la prima parte sono riuscita a fare ma nella seconda parte dove devo trovare la legge oraria di t da 0 a 10s, sono riuscita a trovare l’accelerazione (0,6m/s^2) ma non capisco come devo trovare x0 e v0. Qualcuno mi aiuta per favore?