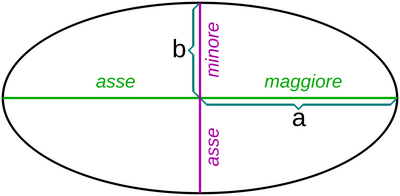
L'orbita di Giove ha un semiasse maggiore pari a $7,784 \times 10^8 km$ e un semiasse minore pari a $7,775 \times 10^8 km$.
Determina:
l'eccentricità dell'orbita di Giove;
la distanza minima e quella massima tra Giove e il Sole.
$$
\left[4,807 \times 10^{-2} ; 7,410 \times 10^5 km ; 8,158 \times 10^8 km \right]
$$
GRAZIE🫶🏿
35
punti
Livello 0
Se indichiamo con a, b la lunghezza del semiasse maggiore e di quello minore, risulta:
e = radice (a² - b²) /a
Sostituendo i valori numerici otteniamo:
e= 4,807*10^(-2)
Il sole è in uno dei fuochi.
Quindi:
d_afelio = a + radice (a² - b²) = 8,158*10^8 km
d_perielio = a - radice (a² - b²) = 7,410*10^8 km
76759
punti
Genius II
L'orbita di Giove ha un semiasse maggiore a pari a 7,784*10^8 km e un semiasse minore b pari a 7,775*10^8 km.
Determina:
# l'eccentricità e dell'orbita di Giove
b^2 = a^2*(1-e^2)
e = √(a^2-b^2)/a^2 = √(1-b^2/a^2) = √ 1-7,775^2/7,784^2 = 0,04807 (4,807*10^-2)
# la distanza massima (afelio) tra Giove e il Sole.
af. = a+√a^2-b^2 = 10^8(7,784+√(7,784^2-7,775^2) = 8,1582*10^8 km
# la distanza minima (perielio) tra Giove e il Sole.
per. = a-√a^2-b^2 = 10^8(7,784-√(7,784^2-7,775^2) = 7,4098*10^8 km
115404
punti
Genius III
In unità di 10^5 km è data l'ellisse praticamente circolare di semiassi (a, b) = (7784, 7775)
* Γ ≡ (x/7784)^2 + (y/7775)^2 = 1
dove la semidistanza focale è
* c = √(a^2 - b^2) = √(7784^2 - 7775^2) = 3*√15559
e l'eccentricità è
* e = c/a = 3*√15559/7784 ~= 151/3141 ~= 0.0480738
e le distanze minima e massima fra un fuoco e i due vertici dell'asse maggiore sono
* min = a - c = 7784 - 3*√15559 ~= 7409.79
* max = a + c = 7784 + 3*√15559 ~= 8158.21
57388
punti
Genius I
