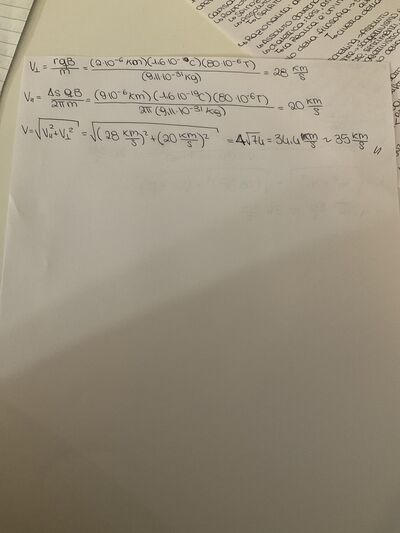Un elettrone si muove in un campo magnetico uniforme di intensità 80 microT. L'elettrone segue un'orbita elicoidale di passo $P=9 mm$ e raggio $=2 mm$. Qual è la velocità dell'elettrone?
$$
\begin{aligned}
& R=\frac{m * v_{\perp}}{q * B} \rightarrow v_{\perp}=\frac{R * q * B}{m}=\frac{2 * 10^{-3} m * 1,6 * 10^{-19} C * 80 * 10^{-6} T }{9,11 * 10^{-31} kg }=28,1 \frac{ km }{ s } \\
& P=v_{\|} * T=v_{\|} * \frac{2 \pi}{\omega}=\frac{v_{\|} * m * 2 \pi}{q * B} \rightarrow v_{\|}=\frac{P * q * B}{m * 2 \pi}=\frac{9 * 10^{-3} m * 1,6 * 10^{-19} C * 80 * 10^{-6} T }{9,11 * 10^{-31} kg * 2 \pi}= \\
& 20,1 \frac{ km }{ s } \\
& v=v_{\|}+v_{\perp}=48,2 \frac{ km }{ s }
\end{aligned}
$$
Questo è il mio ragionamento. Ma come risultato corretto mi da 35 km/s.