[Risolto] Fisica

La pendenza è negativa;

Il valore della pendenza è dato:  -(12m/s)/40m = - 0,3 s^-1

Dal grafico si evince che la distanza percorsa quando v = 4m/s  è circa 27 m

Se ancora rammenti la mia risposta che ti rese felice tre giorni fa
http://www.sosmatematica.it/forum/postid/162297/
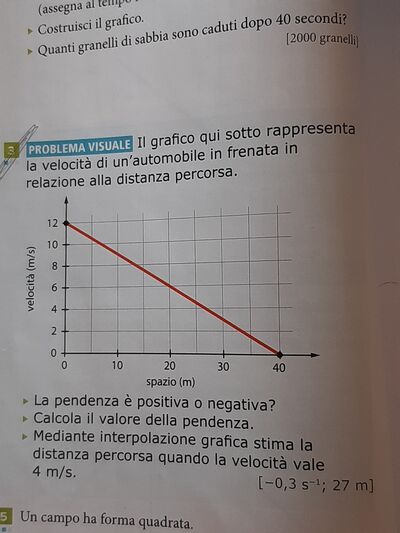
il grafico di questa retta (velocità in funzione della posizione) che taglia entrambi gli assi è del tipo SETTE.
---------------
Come ti scrissi in quel promemoria generale (che dovresti avere stampato, ritagliato, e messo in un quaderno) ...
1) per tracciarlo si congiungono i punti (0, - c/b) e (- c/a, 0), che qui sono (0, 12) e (40, 0)
2) ed ha pendenza m = - a/b, che qui è m = - (12 m/s)/(40 m) = - 3/(10 s) negativa.
Dal tipo-7 si ha
* (- c/b = 12) & (- c/a = 40) & (- a/b = - 3/10) ≡ (a != 0) & (b = 10*a/3) & (c = - 40*a)
e si può, per a = 1, ricavare l'equazione del grafico
* 3*x + 10*y - 120 = 0 ≡ v = 12 - (3/(10 s))*(x m) m/s ≡ x = 40 - (10*v m/s)/3 m
---------------
Il terzo quesito ha due possibili risposte in quanto la consegna e il risultato atteso sono in contraddizione.
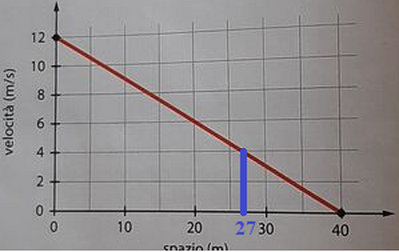
Per rispettare la consegna: quando la velocità è v = 4 m/s la posizione x stimata per interpolazione grafica è "fra 25 e 27.5 m" in quanto, secondo il mio corso di Fisichetta Uno, è scorretto tentare di stimare ad occhio un intervallo minore di mezza tacca.
Per ottenere il risultato atteso: x = 40 - (10*4)/3 = 80/3 = 26.(6) m
---------------
CONCLUSIONE
Il risultato atteso (27 m), oltre ad essere concettualmente scorretto in quanto contraddice la consegna di "stimare" cioè di dare un intervallo e non un valore, è anche numericamente errato in quanto approssimato ingiustificatamente.