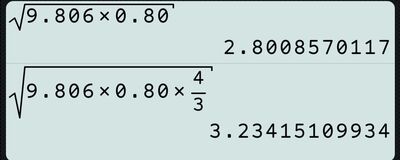Un cilindro pieno ed uno vuoto di uguale massa e raggio pari a 7,5 cm , scendono lungo un piano inclinato partendo da fermi da un'altezza di 0,80 mt. Con moto di puro rotolamento, proseguono lungo un tavolo orizzontale ed infine cadono dal bordo del tavolo da un altezza di 1 mt. Determinare la distanza sul pavimento dei punti di arrivo.
17
punti
Livello 0
Trovata la soluzione :
Compiendo i due satelliti A e B due orbite circolari abbiamo che la costante gravitazionale
a^3/T^2 del satellite A = a^3/T^2 del satellite B = 1
Per cui ra/rb= radice cubica di 9 = circa 2.08
Cilindro cavo
I= momento d'inerzia = MR²
E= (1/2)*I*w² + (1/2)*M*v² = Mv²
Conservazione dell'energia meccanica
M*v² = Mgh
vf1=radice (gh) = 2,80 m/s
Cilindro pieno
I= momento d'inerzia = (1/2)*MR²
E= (1/2)*I*w² + (1/2)*M*v² = (3/4)*M*v²
Conservazione dell'energia meccanica:
vf2= radice [(4/3)*g*h] = 3,23 m/s
Moto parabolico: composizione di due moti:
Moto rettilineo uniforme lungo l'asse x
Moto rettilineo uniformemente accelerato lungo l'asse y con velocità iniziale nulla. Dalla legge oraria del moto si ricava il tempo di volo:
t= radice (2h/g) = 0,45 s
(stesso tempo di volo)
Gittata:
xG1= vf1*t
xG2 = vf2*t
76753
punti
Genius II
tempo di caduta t = √2h/g = √1/4,903 = 0,4516 s
cilindro omogeneo
Ek = (1/2+1/4)m*V^2 = 0,75 m*V^2 = m*g*h
la massa m si elide
velocità V = √0,80*9,806*4/3 = 3,234 m/s
distanza d = t*V = 3,234*0,4516 = 1,461 m
cilindro interamente cavo
E'k = (1/2+1/2) m*V'^2 = m*g*h
la massa m si elide
velocità V' = √0,80*9,806 = 2,801 m/s
distanza d' = t*V' = 2,801*0,4516 = 1,265 m
114205
punti
Genius II
