FIGURA DEL PROBLEMA

Question

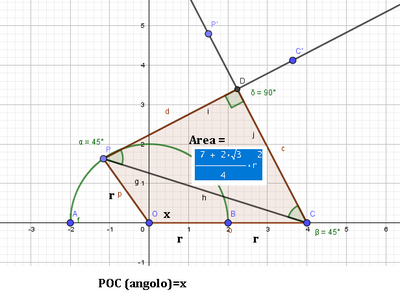
Considera una semicirconferenza di diametro $A B$, centro $O$ e raggio $r$. Sul prolungamento di $A B$ dalla parte di $B$, sia $C$ il punto tale che $\overline{B C}=r$. Considera un punto $P$ sulla semicirconferenza e costruisci il triangolo rettangolo $P C D$, isoscele sulla base $P C$, il cui vertice $D$ giace dalla parte opposta di $A$ rispetto alla retta $P C$. Determina l'angolo $P \widehat{O C}$ in modo che l'area del quadrilatero $O C D P \operatorname{sia}\left(\frac{7+2 \sqrt{3}}{4}\right) r^{2}$.
$[$ Posto $\widehat{\mathrm{POC}}=x, \operatorname{con} 0 \leq x \leq \pi$,
si giunge all'equazione $2 \sin x-2 \cos x=1+\sqrt{3} ;$ il problema ha due soluzioni: $x=\frac{2 \pi}{3} \vee x=\frac{5 \pi}{6}$

Ciao! Potreste rappresentarmi la figura che il problema delinea? Grazie in anticipo

Autore

Risposta

giovanni33333

(@giovanni33333)

8 punti

livello:

Livello 0

2 Risposte
2 0 0

01/02/2022 16:23

LucianoP · Accepted Answer

@giovanni33333

Ciao. Penso di saperti aiutare.

Hai fatto la seguente richiesta:

"Potreste rappresentarmi la figura che il problema delinea?" In base al testo, a meno di mie cattive interpretazioni, la figura che devi fare è quella riportata sotto. Fammi sapere!!!!

Con il teorema di Carnot determino la diagonale PC del quadrilatero:

PC=√(r^2 + (2·r)^2 - 2·r·(2·r)·COS(x))= √(5·r^2 - 4·r^2·COS(x))

Determino quindi la superficie del triangolo PCO:

S1 = r·(2·r)·SIN(x)/2 =r^2·SIN(x)

Determino i cateti dell’altro triangolo rettangolo isoscele:

PD=DC=√2/2·√(5·r^2 - 4·r^2·COS(x))

Determino la sua superficie.

S2=s = 1/2·(√2/2·√(5·r^2 - 4·r^2·COS(x)))^2=s = r^2·(5 - 4·COS(x))/4

Quindi pongo la superficie S1+S2 del quadrilatero pari a:

r^2·SIN(x) + r^2·(5 - 4·COS(x))/4 = (7 + 2·√3)/4·r^2

Si perviene quindi alla equazione lineare in seno e coseno:

- 4·COS(x) + 4·SIN(x) + 5 = 2·√3 + 7

Che fornisce soluzione: x = 5·pi/6 ∨ x = 2·pi/3

LucianoP

(@lucianop)

94792 punti

livello:

Genius II

16803 Risposte
5 5764 3472

08/02/2022 19:04

[Risolto] FIGURA DEL PROBLEMA

Domande