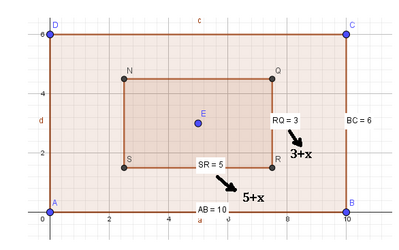
Al centro di una piazza rettangolare lunga 10 m e larga 6 m, si trova un'aiuola, anch'essa rettangolare, con le dimensioni dimezzate rispetto a quelle della piazza. Si vuole ingrandire l'aiuola, aumentando le dimensioni della sua recinzione di una stessa quantità $x$ espressa in metri. I tecnici del Comune pongono come vincolo che l'area occupata dall'aiuola sia maggiore dei $\frac{77}{240}$ della superficie della piazza, ma minore dei $\frac{2}{5}$ della stessa. Di quanto è possibile aumentare le dimensioni della recinzione dell'aiuola?
$$
\left[\frac{1}{2}<x<1\right]
$$