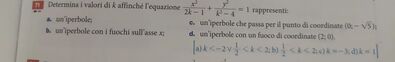@gf
Ciao e ciao a tutti gli amici.
Una iperbole può essere delle due forme:
x^2/a^2 - y^2/b^2 = 1 nel qual caso ha vertici e fuochi sull'asse delle x
oppure
x^2/a^2 - y^2/b^2 = -1 nel qual caso ha vertici e fuochi sull'asse delle y
Quindi, per essere iperbole, si deve avere:
(2·k - 1)·(k^2 - 4) < 0
ossia :
1°F
--------------(1/2)++++++++++>k
2° F
+++(-2)--------------(+2)++++++>k
Segno prodotto:
-----(-2)+++(1/2)---(+2)++++++>k
quindi: k < -2 ∨ 1/2 < k < 2 per questi valori si ha una iperbole.
--------------------------------------------------------------------------
Se i fuochi stanno sull'asse delle x deve essere:
a^2>b^2
quindi due condizioni a sistema.
{k < -2 ∨ 1/2 < k < 2 (determinata sopra)
{2·k - 1 > k^2 - 4
Se risolviamo la seconda abbiamo:
{k < -2 ∨ 1/2 < k < 2
{-1 < k < 3
quindi la soluzione fornisce:
1/2 < k < 2
------------------------------------------------------------
Se l'iperbole passa per il punto (0, - √5)
0^2/(2·k - 1) + (- √5)^2/(k^2 - 4) = 1------> 5/(k^2 - 4) = 1 con k^2 - 4 ≠ 0
quindi: k ≠ -2 ∧ k ≠ 2 si ha:
5 = k^2 - 4--------> k = -3 ∨ k = 3 quindi deve essere k = -3 per poter essere anche una iperbole!
-----------------------------------------------------------------
Ora smetto: l'ultimo quesito rispondo dopo.
Riprendo: c^2 = a^2 + b^2
Quindi 2·k - 1+(4-k^2)= 2^2--------> k = 1
Tenendo presente che k^2-4 è al denominatore di -x^2/b^2
Per k=1
x^2/(2·1 - 1) + y^2/(1^2 - 4) = 1------>x^2 - y^2/3 = 1
controlla su properties al link:
https://www.wolframalpha.com/input/?i=x%5E2-y%5E2%2F3%3D1