Esercizio successioni

Question

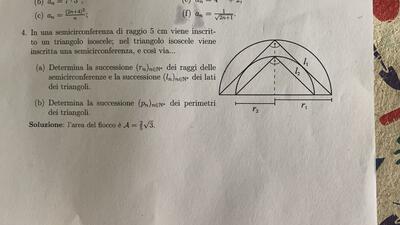
In una semicirconferenza di raggio 5 cm viene inscritto un triangolo isoscele; nel triangolo isoscele viene inscritta una semicirconferenza, e così via...

(a) Determina la successione $\left(r_{n}\right)_{n \in \mathbb{N}^{*}}$ dei raggi delle semicirconferenze e la successione $\left(l_{n}\right)_{n \in \mathbb{N}^{*}}$ dei lati dei triangoli.

(b) Determina la successione $\left(p_{n}\right)_{n \in \mathbb{N}^{*}}$ dei perimetri dei triangoli.
Soluzione: l'area del fiocco è $\mathcal{A}=\frac{2}{5} \sqrt{3}$.

Potete aiutarmi a svolgere questo esercizio per favore

Autore

Risposta

Rui

(@rui)

7 punti

livello:

Livello 0

5 Risposte
4 0 1

06/11/2020 20:35

exProf · Accepted Answer

Nel cerchio di raggio R si inscrive un quadrato di lato
* L = (√2)*R [R = L/√2]
Nel quadrato di lato L si inscrive un cerchio di raggio
* R' = L/2 = R/√2
Nel cerchio di raggio R' si inscrive un quadrato di lato
* L' = (√2)*R' = (√2)*R/√2 = R = L/√2
---------------
Entrambe le successioni richieste hanno la forma della stessa progressione geometrica di ragione 1/√2
* (a(k + 1) = a(k)/√2) & (a(0) = A) ≡
≡ a(k) = A*2^(- k/2)
ma con fattori di forma A diversi.
---------------
Per i raggi delle semicirconferenze, A = 5 cm.
Per i lati dei semiquadrati, A = 5/√2 cm.
---------------
Le successioni richieste sono
* R(k) = 5*2^(- k/2) cm.
* L(k) = 5*2^(- (k + 1)/2) cm.
==============================
Sono lietissimo di apprendere che l'area del fiocco sia già A = 2*√3/5 e ti prego di augurarle da parte mia di crescere ancora in bellezza e saggezza. Ti prego anche di porgere al fiocco le mie più vive e sincere congratulazioni, e figli maschi!
AD MAIORA!

exProf

(@exprof)

57382 punti

livello:

Genius I

13649 Risposte
37 3107 1795

07/11/2020 00:35

[Risolto] Esercizio successioni

Domande