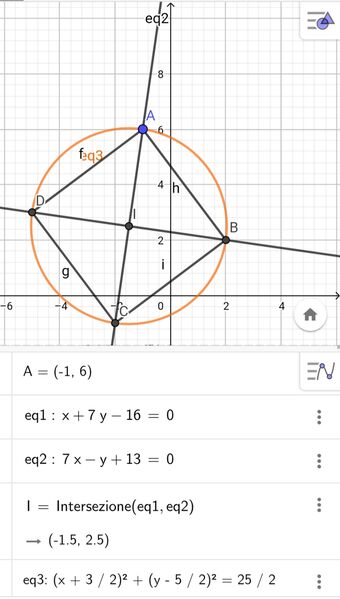
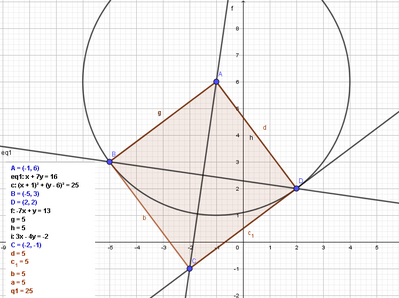
Siano A B C D i vertici di un quadrato nel piano cartesiano. Sapendo che A (-1;6) e che la diagonale BD ha equazione x + 7y - 16 = 0 determinare le coordinate di B,C,D,.
Sul testo che ha pubblicato l'esercizio non c'è la risposta. Ringrazio tutti come sempre per l'aiuto che mi date e chiedo cortesemente, se possibile, di spiegare nel dettaglio passaggio per passaggio.