[Risolto] Esercizio equazione della parabola

Ogni parabola Γ con
* asse di simmetria parallelo all’asse y
* apertura a != 0
* vertice V(w, h)
ha
* equazione Γ ≡ y = a*(x - w)^2 + h
* pendenza m(x) = 2*a*(x - w)
---------------
Il passaggio per l'origine impone il vincolo
* 0 = a*(0 - w)^2 + h ≡ h = - a*w^2
da cui
* Γ ≡ y = a*(x - w)^2 - a*w^2 ≡ y = a*x*(x - 2*w)
---------------
La pendenza "nel suo punto di ascissa 4" è
* m(4) = a*(8 - 2*w)
------------------------------
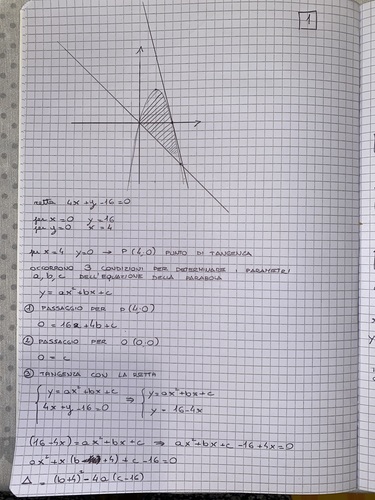
La retta
* 4*x + y - 16 = 0 ≡ y = - 4*(x - 4)
ha pendenza
* m = - 4
e, "nel suo punto di ascissa 4", ha ordinata zero.
Quindi il punto di tangenza è T(4, 0).
La condizione di tangenza è
* m(4) = m ≡ a*(8 - 2*w) = - 4 ≡ w = 2*(2*a + 1)/a
da cui
* Γ ≡ y = a*x*(x - 2*w) = a*x*(x - 2*2*(2*a + 1)/a) ≡ y = a x^2 - 4*(2*a + 1)*x
------------------------------
Il passaggio per T(4, 0) impone il vincolo
* 0 = a 4^2 - 4*(2*a + 1)*4 ≡ a = - 1
da cui
* w = 2*(2*(- 1) + 1)/(- 1) = 2
* h = - (- 1)*2^2 = 4
e infine
* Γ ≡ y = 4 - (x - 2)^2
------------------------------
VERIFICA al link
http://www.wolframalpha.com/input/?i=%284*x%2By-16%3D0%29%26%28y%3D4-%28x-2%29%5E2%29