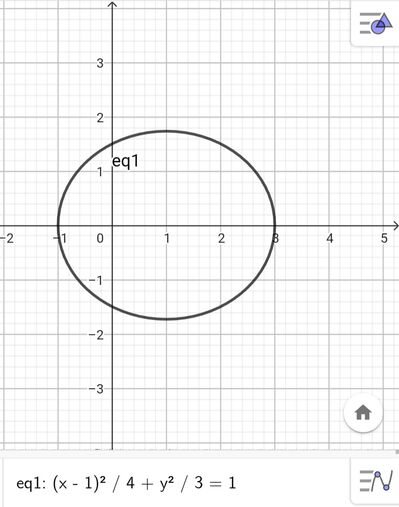
Si determini il luogo dei punti $P$ del piano tali che $d(P, F)=\frac{1}{2} \cdot d(P, r)$, dove $F(0,0)$ e $r: x=-3$.
[R. Il luogo richiesto è l'ellisse di equazione $3 x^2+4 y^2-6 x-9=0$, che ammette forma canonica $\frac{(x-1)^2}{4}+\frac{y^2}{3}=1$ ]
3
punti
Livello 0
Le distanze del generico punto P(x;y) da F ed r sono:
d(P;F) = radice (x²+y²)
d(P;r) = |x+3|
Imponendo la condizione richiesta:
radice (x²+y²) =(1/2)* |x+3|
Elevando a quadrato entrambi i membri:
x²+y²=(1/4)*(x+3)²
3x²+4y²-6x=9
3(x-1)²+ 4y²=12
[(x-1)²/4] + y²/3 = 1
Ellisse di centro C(1;0)
Asse maggiore asse x => V1(-1;0),V2(3;0)
Asse minore x=1 => V3(1; - rad 3),V4(1;rad 3)
76754
punti
Genius II
