Per quanto sia semplice non riesco a svolgere questo esercizio 🙁 :
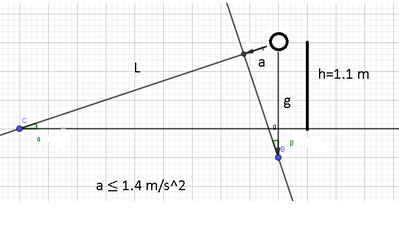
Per fare scendere dei barili da un ripiano a 1,1 m da terra con accelerazione minore di 1.4 m/s^2, si deve preparare un'asse di legno come scivolo.
Calcola la lunghezza minima dell'asse di legno.
(7,7 m)
Grazie mille in anticipo!