Fra tutte le circonferenze tangenti al punto T(1;1) alla bisettrice del I e III quadrante, determina quelle che sono tangenti alla bisettrice del II e IV quadrante.
Risposte : x^2 + y^2 - 4x + 2 = 0 ; x^2 + y^2 - 4y + 2 = 0.
Grazie come sempre per il vostro aiuto e le indicazioni che mi fornite per comprendere l'eesercizio.
1502
punti
Livello 1
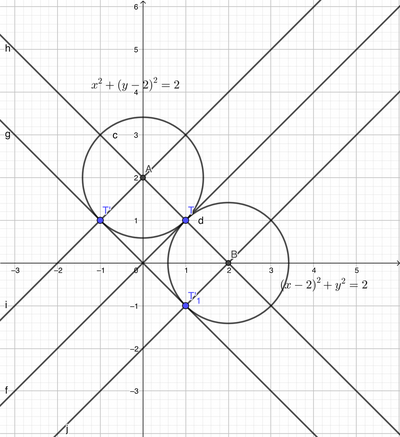
Essendo le circonferenze tangenti nel punto (1,1) alla bisettrice del I, III quadrante, per le proprietà geometriche della conica (raggio vettore perpendicolare alla retta tangente nel punto) possiamo dire che il centro C delle circonferenze sarà sulla retta y= - x + 2 (retta perpendicolare alla bisettrice y=x e passante per il punto di tangenza). Quindi le coordinate del centro delle circonferenze che vogliamo trovare sono:
C=(xc, - xc + 2)
Sappiamo inoltre che le circonferenze sono tangenti alla bisettrice dei quadranti pari. Devono quindi avere raggio:
R= radice (2)
che rappresenta la distanza della retta y= - x + 2 (retta a cui appartiene il centro C) dalla bisettrice y= - x
Possiamo quindi scrivere l'equazione delle circonferenze
(x - xc) ² + (y - ( - xc + 2)) ² = (radice (2))²
(x - xc) ² + (y + xc - 2)² = 2
Imponendo la condizione di appartenenza del punto (1,1) posso determinare i valori di xc.
Dalla condizione di appartenenza del punto alla conica, risulta:
(1 - xc) ² + (xc - 1)² = 2
2xc² - 4xc = 0
Da cui si ricava
xc=0 ==> yc=2
xc=2 ==> yc=0
Le circonferenze hanno quindi centro
C1=(0, 2) ; R = radice (2)
C2=(2,0) ; R = radice (2)
76753
punti
Genius II
Grazie come sempre per la tua puntualità, chiarezza e semplicità nella spiegazione dei vari passaggi. Buona giornata anche a te e buon lavoro.
Fa piacere leggere che le spiegazioni ti risultano chiare! Complimenti per la costanza e la determinazione! Buona giornata
@stefanopescetto 👍 👍 👍
94701
punti
Genius II
Ogni circonferenza tangente due rette incidenti è centrata sulle loro bisettrici.
Gli assi coordinati sono bisettrici delle loro bisettrici.
Quindi ogni circonferenza tangente le bisettrici dei quadranti è centrata sugli assi.
Per la simmetria dovuta all'avere in comune il punto di tangenza T(1, 1) le due circonferenze devono avere lo stesso raggio e i centri equidistanti dall'origine: r, (k, 0) e (0, k).
* Γ1 ≡ (x - k)^2 + y^2 = q = r^2
* Γ2 ≡ x^2 + (y - k)^2 = q = r^2
------------------------------
I valori di k e q si determinano dai vincoli d'appartenenza di T alle circonferenze e alla congiungente (x/k + y/k = 1) dei centri
* ((1 - k)^2 + 1^2 = q) & (1^2 + (1 - k)^2 = q) & (1/k + 1/k = 1) ≡
≡ (k = 2) & (q = 2)
da cui
* Γ1 ≡ (x - 2)^2 + y^2 = 2 ≡ x^2 + y^2 - 4*x + 2 = 0
* Γ2 ≡ x^2 + (y - 2)^2 = 2 ≡ x^2 + y^2 - 4*y + 2 = 0
che è proprio il risultato atteso.
57383
punti
Genius I
@exprof 👍 👍 👍
