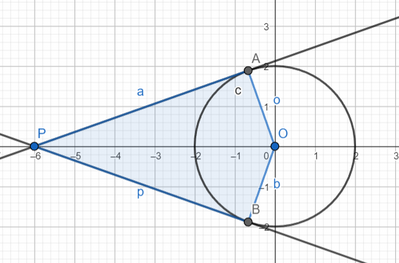
Da un punto P, esterno alla circonferenza di centro O, tracciamo le tangenti che toccano la circonferenza nei punti A e B. Calcola le misure degli angoli e il perimetro del quadrilatero PBOA sapendo che le distanze di P da O e da A sono rispettivamente 32 cm e 27,71 cm e che l'angolo POA ha ampiezza di 60°.
Risultato:
(90°; 90°; 60°; 120°; 87,42 cm)
139
punti
Livello 1
Gli angoli in A e B sono retti perché le tangenti sono perpendicolari ai raggi.
L'angolo BOA=120 perché PO è bisettrice.
Per la somma degli angoli interni di un quadrilatero dev'essere:
P=360-120-90-90= 60
Per Pitagora:
$AO = \sqrt{PO^2-PA^2}= \sqrt{32^2-27.71^2}=16$
dunque:
$ p = 2(AO+AP) = 2(16+27.71)= 87.42 cm$
Noemi
9874
punti
Livello 5
